中学数学建模方法-固定起点最短路问题

一、固定起点的最短路

若给出了一个连接若干个城镇的铁路网络，在这个网络的两个指定城镇间，找一条最短铁路线.

以各城镇为图G的顶点，两城镇间的直通铁路为图G相应两顶点间的边，得图G.对G的每一边e，赋以一个实数w( e)，即直通铁路的长度，称为e的权，得到赋权图G.G的子图的权是指子图的各边的权和.问题就是求赋权图G中指定的两个顶点u 0 ，v0间的具最小权的轨，这条轨叫做u 0 ，v0间的最短路，它的权叫做u 0 ，v0间的距离，亦记作d (u 0 ，v0).求固定起点的最短路已有成熟的算法——迪克斯特拉（Dijkstra）算法.

（1）Dijkstra算法的基本思想.

按距u0从近到远，依次求得u0到G的各顶点的最短路和距离，直至v0（或直至G的所有顶点），算法结束.为避免重复并保留每一步的计算信息，采用了标号算法.

（2）Dijkstra算法的步骤.

①令l (u0)=0，对v ≠u0，令l (v)=∞，S0={u0}，i=0.

②对每个用

代替l(v).计算，把达到这个最小值的一个顶点记为1iu+，令.

③若i =|V|-1，停止；若i ＜|V|-1，用i+1代替i，转②.

算法结束时，从u0到各顶点v的距离由v的最后一次的标号l (v)给出.在v进入Si之前的标号l (v)叫T标号，v进入Si时的标号l (v)叫P标号.算法就是不断修改各项点的T标号，直至获得P标号.若在算法运行过程中，将每一顶点获得P标号所由来的边在图上标明，则算法结束时，u0至各项点的最短路也在图上标示出来了.

例1　某公司在6个城市c1 ，c2，…，c6中有分公司，从ci到cj的直接航程票价记在下述矩阵A的(i， j)位置上（∞表示无直接航线），请帮助该公司设计一张由城市c1到其他城市间的票价最便宜的路线图.

用矩阵An ×n(n为顶点个数)存放各边权的邻接矩阵，行向量d (i)，index2 (i)分别存放始点到第i点最短通路的值和始点到第i点最短通路中第i顶点前一顶点的序号.求第一个城市到其他城市的最短路径的MATLAB程序如下：

运行结果为：

由结果知c1到c4最便宜的路线是1→6→4（票价35），而不是直接从c1到c4（票价40）；c1到c3最便宜的路线是1→5→3（票价45）；c1到c2最便宜的路线是1→6→2（票价35）.

例2（安全渡河问题的最短路解法）第四章第一节安全渡河问题可先建立图的模型，再移植Dijkstra算法加以解决.

如图8.2.1所示，将两岸安全状态设为点，分别称为计划过河状态和计划返回状态，这两种状态通过决策向量来实现相互转化.把能够相互转化的状态间连线表示，得到此状态转移关系图，此时问题转化为求起点（计划过河状态(3，3)）到终点（计划返回状态(0，0)）间的最短路，通过Dijkstra算法即可求得[4].

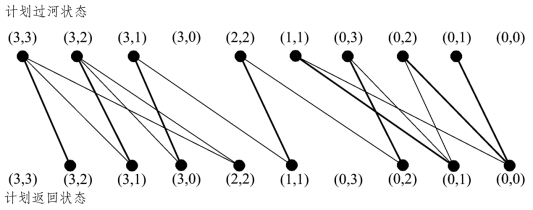
图8.2.1　状态转移关系图

求解程序如下：

function process=cross_river(n1,n2,n3)

%生成决策矩阵;

%生成安全状态矩阵;

%生成邻接矩阵;

% dijkstra算法;

%生成最优状态转移矩阵;

二、每对顶点之间的最短路

计算赋权图中每对顶点之间的最短路径，显然可以调用Dijkstra算法，这种方法的时间复杂度为O (n3).解决这一问题的恰当方法是佛洛伊德（Floyd）算法.

（1）Floyd算法的基本思想.

直接在图的赋权邻接矩阵中用插入顶点的方法依次构造出n个矩阵D(1)，D(2)，…，D(n)，最后得到的矩阵D(n)成为图的距离矩阵，同时也求出插入点矩阵以便得到两点间的最短路径.

（2）Floyd算法原理.

①求距离矩阵的方法.

步骤1：把赋权邻接矩阵A作为距离矩阵的初值，即

步骤2：其中是从vi到vj的只允许以v1作为中间点的路径中最短路的长度.

步骤3：其中是从vi到vj的只允许以v1，v2作为中间点的路径中最短路的长度.

……

步骤n+1：其中是从vi到vj的只允许以v1，v2，…，vn作为中间点的路径中最短路的长度，即从vi到vj中间可插入任何顶点的路径中最短路的长度，因此D(n)为距离矩阵.

②求路径矩阵的方法.

在建立距离矩阵的同时可建立路径矩阵的含义是从vi到vj的最短路要经过点号为rij的点.

每求得一个D(k)时，按下列方式产生相应的新的R(k)：

(www.xing528.com)

即当vk被插入任何两点间的最短路径时，被记录在R(k)中，依次求D(n)时求得R(n)，可由R(n)来查找任何点对之间最短路的路径.

③查找最短路路径的方法.

若，则点p1是点i到点j的最短路的中间点，然后用同样的方法再分头查找.若：

a.向点i追溯得：

b.向点j追溯得：

则由点i到j的最短路的路径为：i，pk，…，p2，p1，q1，q2，…，qm，j.

（3）Floyd算法步骤.

dij：i到j的距离.

rij：i到j之间的插入点.

输入带权邻接矩阵W：

①赋初值：对所有i，j，d(i，j)←w(i，j)，r(i，j)←j，k←1.

②更新d(i，j)，r(i，j)：对所有i，j，若d(i，k)+d(k，j)＜d(i，j)，则d(i，j)←d(i，k)+d(k，j)，r(i，j)←k.

③若k=n，停止；否则k←k+1，转②.

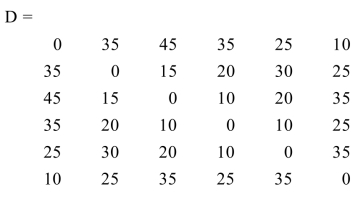
例3　用Floyd算法求解例1.

矩阵D为任意两点间的最短距离，矩阵R用来存放每对顶点之间最短路径上所经过的顶点的序号.Floyd算法的MATLAB自定义函数floyd.m如下：

求解例1的主程序：

运行结果如下：

三、应用——选址问题

选址问题是指为一个或几个服务设施在一定区域内选定它的位置，使某一指标达到最优值.选址问题的数学模型依赖于设施可能的区域和评判位置优劣的标准，有许多不同类型的选址问题.在此只简单介绍服务设施与服务对象都位于一个图的顶点上的单服务设施问题.

1.中心问题

有些公共服务设施（例如一些紧急服务型设施如急救中心、消防站等）的选址，要求图中最远的被服务点离服务设施的距离尽可能地小.

例4　某城市要建立一个消防站，为该市所属的七个区服务（见图8.2.2）.问：应设在哪个区，才能使它至最远区的路径最短？

图8.2.2　七个区间的交通图

算法：

（1）用Floyd算法求出距离矩阵D=(dij )n× n .

（2）计算在各点vi设立服务设施的最大服务距离S(vi)：

（3）求出顶点kv，使则kv就是要求的建立消防站的地点.此点称为图的中心点.

对此问题，用MATLAB编写主程序road1.m如下：

运行road1.m（需调用前面介绍的floyd.m），得结果：

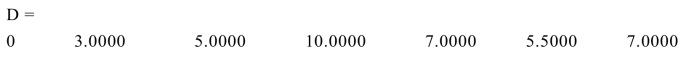
故得：S(v1)=10，S(v2)=7，S(v3)=6，S(v4)=10，S(v5)=7，S(v6)=7，S(v7)=8.5，因S(v3)=6为最小，故应将消防站设在v3处.

2.重心问题

有些设施（例如一些非紧急型的公共服务设施，如邮局、学校等）的选址，要求设施到所有服务对象点的距离总和最小.一般要考虑人口密度问题，要使全体被服务对象来往的平均路程最短.

例5　某矿区有七个矿点（见图8.2.3），已知各矿点每天的产矿量q(vj)（标在图8.2.2的各顶点上）.现要从这七个矿点选一个来建选矿厂，问应选在哪个矿点，才能使各矿点所产的矿石运到选矿厂的总运力（单位：kt·km）最小？

图8.2.3　七个矿点间的交通图

算法：

（1）求距离矩阵D=(dij )n× n .

（2）计算各顶点作为选矿厂的总运力m(vi)：

（3）求kv，使，则kv就是选矿厂应设之矿点.此点称为图G的重心或中心点.

对此问题，用MATLAB编写主程序road2.m如下：

运行road2.m（需调用前面介绍的floyd.m），得结果：

故应将选矿厂设在v3处.