柔性机构动态可靠性分析成果

柔性机构为非线性系统,动态响应的随机过程很复杂,只能进行相应的简化才可以获得整个运动时域内极值的分布特性。通过各个单位时间段动态响应的分布特性对整个运动时域的极值分布进行参数估计,这种方法的实质是将运动时域内的动态响应看作单位时间段动态响应的串联。随机变量当量正态变换的方法已经较为成熟^[165-168],经过当量正态变换以后确定动态响应极值的概率分布。

假设在单位时间段τ=T/n上的动态响应X(t_i)出现的概率为P^*(t_i),X(t_i)表示第i个发生的动态响应大小,独立分布于F(x),令X(t₀)=0。

从动态响应X(t_i-1)发生到X(t_i)发生所经历的时间段个数为随机变量,记为X_i,假设X_i独立同服从于参数λ的泊松分布,则X_i为随机变量序列,即

式中,k=0,1,2,…;i=1,2,3,…;λ＞0。

令

式中 W_n——前n个动态响应所经历的时段总数,显然W₀=0。

第n个动态响应发生的时刻为τ_n。

W_n服从于参数为nλ的泊松分布,即

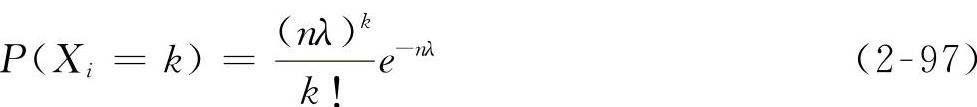
令

N(t)=max{n:W_n≤t} (2-98)

则N(t)为一个泊松更新过程,{X_iτ}为更新间距,{X_iτ}为更新时刻。

令

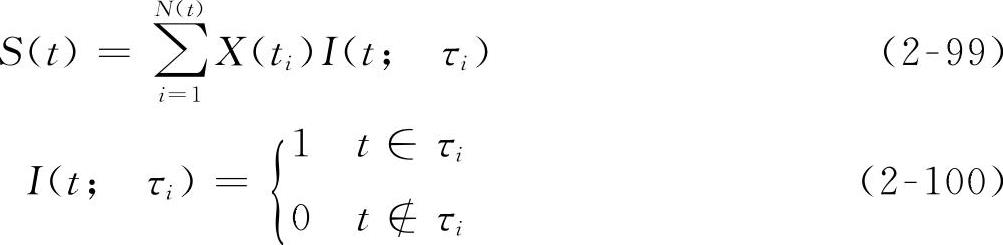
式中 τ_i——第i次动态响应的持续时间;

X(t_i)——动态响应的截口随机变量。

如果上述条件满足,则S(t)为一个复合泊松更新过程^[166-168],如图2-15所示。

如果动态响应满足复合泊松更新过程,在柔性机构运动时域内,设动态响应的极值为

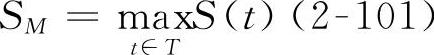
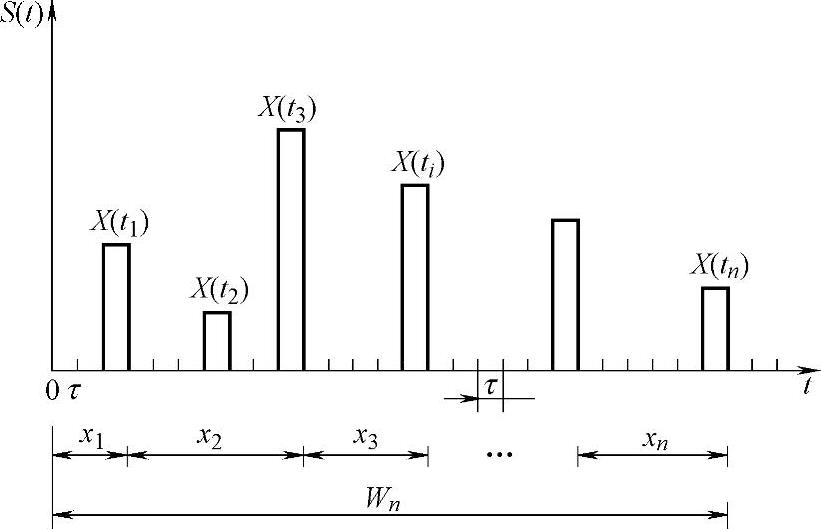
图2-15 动态响应的泊松随机过程(www.xing528.com)

则S_M的概率分布为^[166]

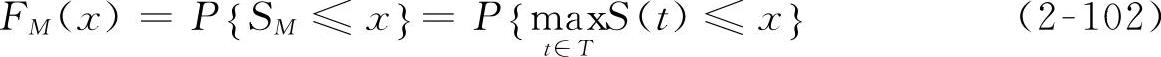
将整个运动时域的分布特性由各个单位时间段的分布特性来表示,则

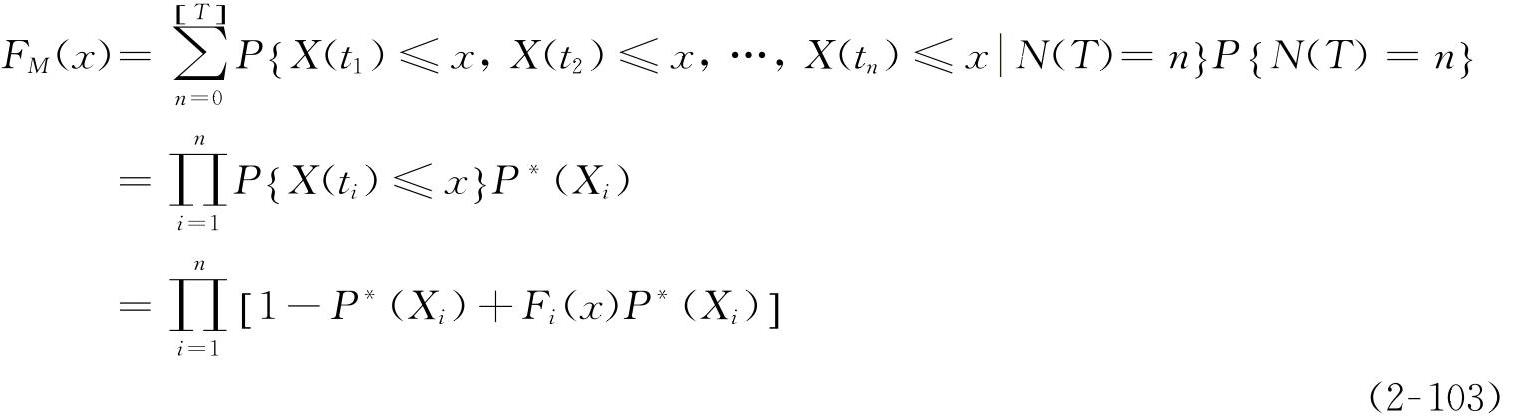
根据柔性机构动力学仿真,可以得到动态响应随机变量在各个时间截口的分布特性。这样,根据上述分析,按照式(2-103)就可以得到动态响应在整个时域内极值的分布特性。特别地,当各个单位时间段动态响应出现的概率为确定值P*时,则随机过程演化为平稳二项分布随机过程,式(2-103)可以改写为

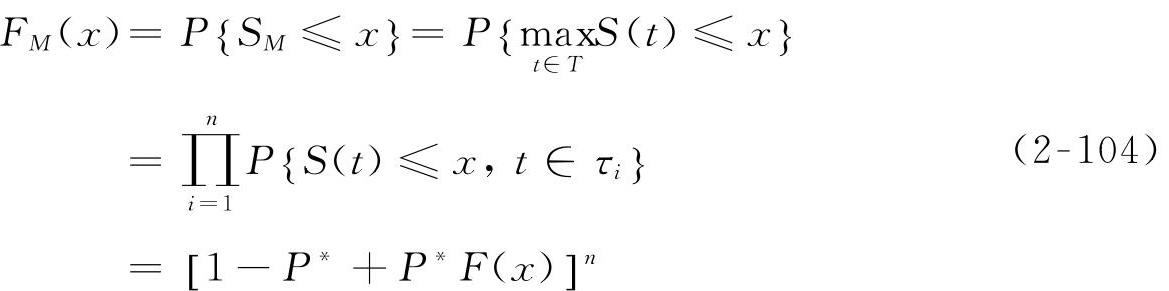
当每个单位时间段都出现动态响应,即P*=1时,则有F_M(x)=[F(X)]ⁿ,动态响应经过当量正态化转换后,若分布特性为(μ,σ²),则

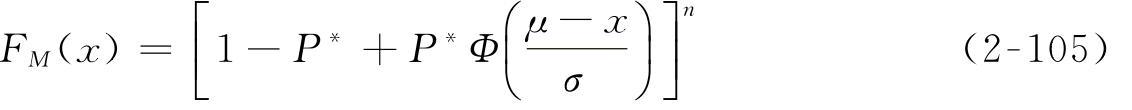
在柔性机构运动时域内,动态响应为一个时间连续的随机过程X(t),如果将X(t)考虑为马尔可夫(Markov)分布的随机过程^[169,170],即将运动时域动态响应随机过程划分为若干个单位时间段,将整个运动时域的运动当作各个单位时间段动态响应的串联,并假设在不同仿真计算中各个单位时间段内柔性机构的拓扑结构变化是相同的。将柔性机构运动时域内的拓扑结构变化看作各个单位时间段的不同拓扑结构的串联,每个单位时间段柔性机构运动包括快变运动和慢变运动,并将快变运动看作随机振动,慢变运动看作随机运动。在单位时间段中动态响应的出现为马尔可夫(Markov)随机过程。

设运动时域T内动态响应随机过程X(t)的状态空间S是有限集,对于任意n+1个参数t₁＜t₂＜t₃＜…＜t_n＜t_n+1以及状态空间S中的任意n+1个状态X(t₁),X(t₂),X(t₃),…,X(t_n),X(t_n+1),如果下列条件概率成立:

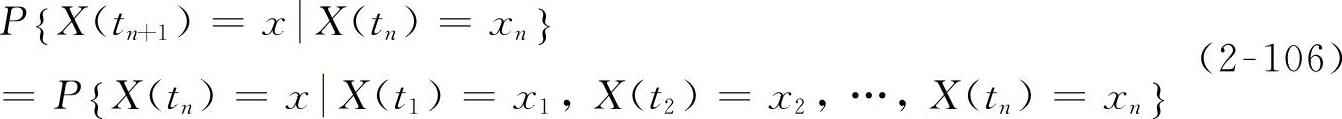
则称这种随机过程为连续时间有限状态的马尔可夫(Markov)过程。其含义是:在已知随机过程现在状态X(t_n)的条件下,将来状态X(t_n+1)的条件概率分布与过去状态X(t₁),X(t₂),X(t₃),…,X(t_n-1)没有直接关系。

在每个单位时间段,动态响应X(t)的出现次数按照马尔可夫(Markov)随机过程分布假设,设动态响应的极值为S_M,根据随机振动理论^[49-51],在单位时间段内动态响应的极值为S_M服从瑞利Rayleigh分布,对于平稳窄带正态分布的动态响应,极值的分布函数F_M(x)为

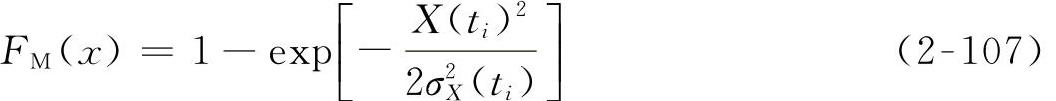
概率密度函数f_M(x)为

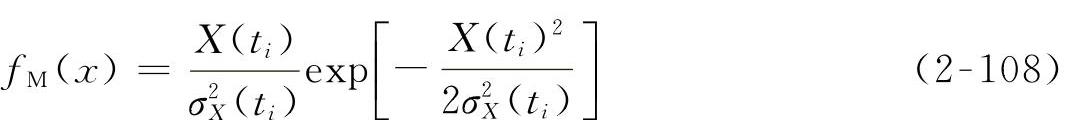
对于非平稳窄带正态分布的动态响应,极值的分布函数F_M(x)为

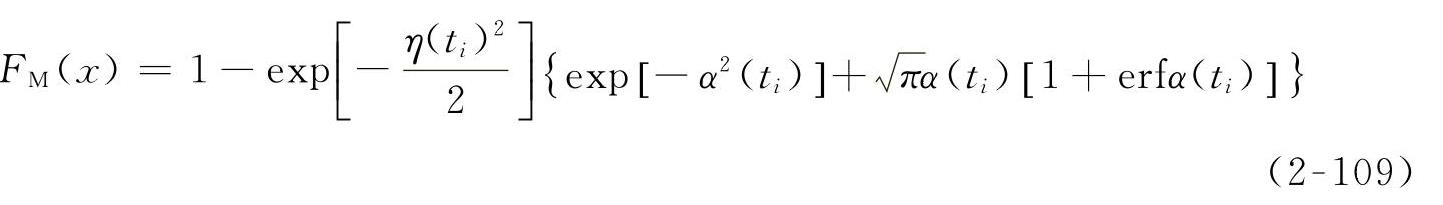
式中

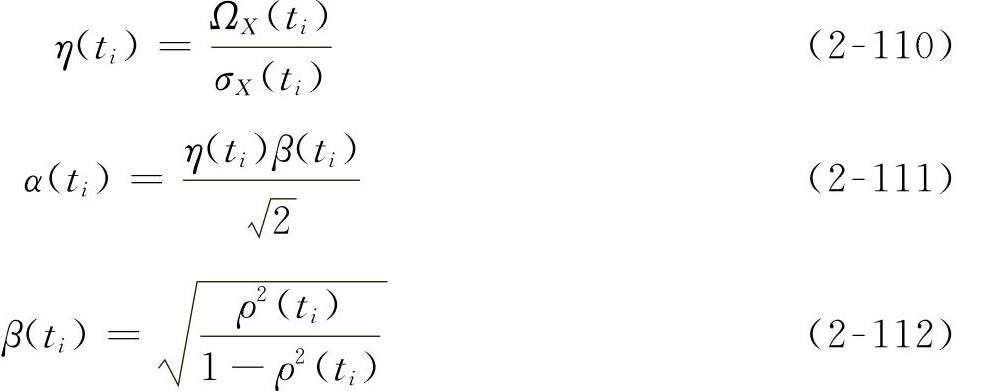
式中,ρ(t_i)为X(t)和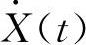的相关系数。

如果随机过程假设为窄带平稳过程,并且X(t)和X·(t)不相关,则:α(t_i)=0,β(t_i)=0,ρ(t_i)=0,代入式(2-104),则得到式(2-102)的形式。