高等数学试题分析（2017）：填空题解析

1．设级数un的部分和数列Sn＝（n＝1，2，…），则级数的一般项un＝________．

解　u1＝S1＝1，n≥2时un＝Sn－Sn－1＝且当n＝1时也成立，故对所有n∈N＊，有un＝

2．幂级数的收敛半径R＝________．

分析　该幂级数是缺项的幂级数（不含x的偶数次幂），因此不能直接利用公式求收敛半径R．

解法一　把该幂级数看成是一般的函数项级数un（x），其中

由

知，当＜1，即｜x｜＜2时，级数绝对收敛；当＞1，即｜x｜＞2时，级数发散．所以，该幂级数的收敛半径R＝2．

解法二　把幂级数改写为

令y＝x2，考虑幂级数，因为

所以，当｜y｜＜4，即｜x｜＜2时，原幂级数绝对收敛；当｜y｜＞4，即｜x｜＞2时，原幂级数发散．所以，原幂级数的收敛半径R＝2．

3．若级数条件收敛，则幂级数nan（x－1）n的收敛区间为_________．

解　幂级数在x＝1处显然收敛，所以其收敛半径R≥1．若R>1，应用阿贝尔定理，可得幂级数在x＝1处绝对收敛，此与条件矛盾，所以R＝1，幂级数的收敛区间为（－1，1），因此幂级数an（x－1）n的收敛区间为（0，2）．由于幂级数逐项求导后收敛半径不变，所以幂级数nan（x－1）n－1的收敛区间是（0，2），因此

的收敛区间也是（0，2）．

4．若幂级数在x＝2处条件收敛，则幂级数（x－1）2n的收敛半径R＝_________．

解　由于anxn的收敛半径为2，于是对于幂级数（x－1）2n而言，当＜2时，级数收敛，当＞2时，级数发散，故（x－1）2n的收敛半径R＝

5．设幂级数的收敛半径为3，则幂级数nan（x－1）n－1的收敛区间为_________．

解　因为幂级数anxn的收敛半径为3，所以幂级数an（x－1）n的收敛半径也为3．由于幂级数在其收敛区间内可以逐项求导，且逐项求导后的幂级数收敛半径不变，故幂级数nan（x－1）n－1＝（an（x－1）n）′的收敛半径仍为3，从而由｜x－1｜＜3得所求的收敛区间为（－2，4）．

6．把函数（ab ≠0）展开成x 的幂级数，其收敛半径R＝_________．

解　因为

由＜1，即｜x｜＜，所以收敛半径R＝

7．幂级数的收敛域为_________．

解　该幂级数的收敛半径R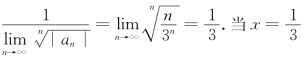＝时，原级数化为调和级数，故发散；当x＝－时，原级数化为交错项级数（－1）n，满足Leibniz判敛法的条件，收敛．故原级数的收敛域为

8．幂级数（－1）n的收敛域为________．

解　该幂级数的收敛半径为

当x＝－2时，原级数为，发散；当x＝2时，原级数为

满足Leibniz判敛法的条件，收敛．故原级数的收敛域为（－2，2］．

9．幂级数（x－1）n的收敛域是________．

解　由于＝0，且是单减数列，由Leibniz判别法得知，收敛．又发散，因此当2｜x－1｜＜1，即｜x－1｜＜时，级数收敛，且当x＝时，级数收敛，当x＝时，级数发散．所以幂级数的收敛域为

10．当常数p满足条件________时，级数绝对收敛．

解　由

知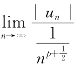＝1，而当且仅当p＋＞1，即p＞时收敛，所以由比较判敛法的极限形式及绝对收敛的定义，知p>时原级数绝对收敛．(https://www.xing528.com)

11．级数的和等于________．

解法一　因为

设S（x）＝，x∈［－1，1），则

于是，所求数项级数的和为2S＝2ln2－1．

解法二　由于ln（1－x）＝－，x∈［－1，1），所以

从而

12．级数的和等于________．

解　因为

由ex＝，x∈（－∞，＋∞）及ln（1＋x）＝，x∈（－1，1］得

从而原级数的和等于2e＋ln2．

13．用sinx ≈x－x3＋…＋计算sin18°，使其误差｜R｜＜10－4，取n＝_________为宜．

解　由交错级数的Leibniz判别法知，余项

以（18°＝弧度）代替x，有｜R2n－1｜≤．若取n＝2，则误差

所以应取n＝2．

14．函数f（x）＝ln（1－x－2x2）关于x 的幂级数展开式中，x3的系数是_________．

解　因为f（x）＝ln（1－x－2x2）＝ln（1＋x）＋ln（1－2x），而

故所求系数是（－1）3－1

15．将f（x）＝1－｜x｜在区间［－1，1］上展开成以2为周期的余弦级数

则其中系数a3的值为_________．

解　f（x）＝1－｜x｜为偶函数，由Euler－Fourier公式得

16．设f（x）＝x2（0≤x≤π），而S（x）＝sinnx，其中

则S（－）＝________，S（π）＝________．

解　题意是将定义在［0，π］上的函数f（x）奇延拓成（－π，π］上的函数F（x），再将F（x）以2π为周期作周期延拓后展开成Fourier级数，即可将f（x）展开成正弦级数．由Dirichlet收敛定理，知

17．已知函数

若S（x）为f（x）的以2π为周期的Fourier级数的和函数，则在区间［－π，π］上S（x）的表达式为_________．

解　由Dirichlet收敛定理，可知当－π＜x＜0及0＜x＜π时，S（x）＝f（x），则

综上知

18．将函数f（x）＝1＋sinx（0≤x≤π）展开为以2π为周期的正弦级数，S（x）为该正弦级数的和函数，则S（ －）＝________，S（3π）＝________．

解　由Fourier级数的Dirichlet收敛定理，可得