回归分析的多元线性回归标准型

1.多元线性回归

回归分析中最简单的形式是y=β0+β1x，x，y均为标量，β0，β1为回归系数，称一元线性回归.它的一个自然推广是x为多元变量，形如

m≥2，或者更一般地

其中x=（x1，…，xm），fj（j=1，…，m）是已知函数.这里y对回归系数β=（β0，β1，…，βm）是线性的，称为多元线性回归.不难看出，对自变量x作变量代换，就可将式（9.4.2）化为式（9.4.1）的形式，所以下面以式（9.4.1）为多元线性回归的标准型.

2.模型

在回归分析中自变量x=（x1，x2，…，xm）是影响因变量y的主要因素，是人们能控制或能观察的，而y还受到随机因素的干扰，可以合理地假设这种干扰服从零均值的正态分布，于是模型记作

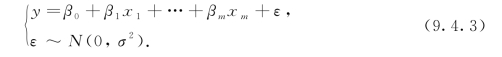
其中σ未知.现得到n个独立观测数据（yi，xi1，…，xim），i=1，…，n，n＞m，由式（9.4.3）得

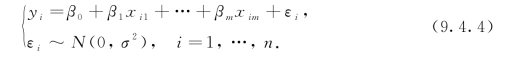
记

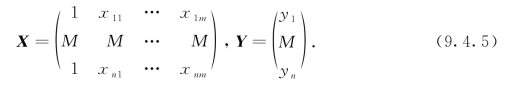
式（9.4.4）表示为

3.参数估计

用最小二乘法估计模型式（9.4.3）中的参数β.由式（9.4.4）这组数据的误差平方和为

求β使Q（β）最小，得到β的最小二乘估计，记作，可以推出

将代回原模型得到y的估计值

而这组数据的拟合值为，拟合误差称为残差，可作为随机误差ε的估计，而

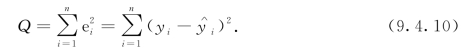
为残差平方和（或剩余平方和），即.

4.统计分析

不加证明地给出以下结果：

（1）是β的线性无偏最小方差估计.指的是是Y的线性函数；的期望等于β；在β的线性无偏估计中，的方差最小.

（2）服从正态分布

（3）对残差平方和Q，EQ=（n-m-1）σ2，且

由此得到σ2的无偏估计

s2是剩余方差（残差的方差），s称为剩余标准差.

（4）对Y的样本方差进行分解，有

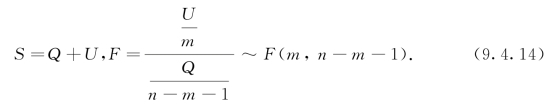
其中Q是由式（9.4.10）定义的残差平方和，反映随机误差对y的影响，U称为回归平方和，反映自变量对y的影响.

5.回归模型的假设检验

因变量y与自变量x1，…，xm之间是否存在如模型式（9.4.1）所示的线性关系是需要检验的，显然，如果所有的都很小，y与x1，…，xm的线性关系就不明显，所以可令原假设为

H0：βj=0（j=1，…，m）当H0成立时由分解式（9.4.14）定义的U，Q满足

在显著性水平α下有1-α分位数F1-α（m，n-m-1），若F＜F1-α（m，n-m-1），接受H0；否则，拒绝.

注意 拒绝H0只说明y与x1，…，xm的线性关系不明显，可能存在非线性关系，如平方关系.

还有一些衡量y与x1，…，xm相关程度的指标，如用回归平方和在样本方差中的比值定义

R∈[0，1]称为相关系数，R越大，y与x1，…，xm相关关系越密切，通常，R大于0.8（或0.9）才认为相关关系成立.

6.回归系数的假设检验和区间估计

当上面的H0被拒绝时，βj不全为零，但是不排除其中若干个等于零.所以应进一步作如下m个检验（j=1，…，m）：.

由式（9.4.11），，cjj是（XTX）-1对角线上的元素，用s2代替σ2，由式（9.4.11）～式（9.4.13），当成立时

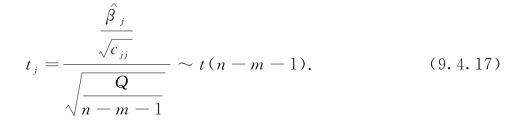
对给定的α，若，接受；否则，拒绝.

式（9.4.17）也可用于对βj作区间估计（j=0，1，…，m），在置信水平1-α下，βj的置信区间为

其中.

7.利用回归模型进行预测

当回归模型和系数通过检验后，可由给定的x0=（x01，…，x0m）预测y0，y0是随机的，显然其预测值（点估计）为

给定α可以算出y0的预测区间（区间估计），结果较复杂，但当n较大且x0i接近平均值时，y0的预测区间可简化为

其中是标准正态分布的分位数.

对y0的区间估计方法可用于给出已知数据残差的置信区间，ei服从均值为零的正态分布，所以若某个ei的置信区间不包含零点，则认为这个数据是异常的，可予以剔除.

8.MATLAB实现

MATLAB统计工具箱用命令regress实现多元线性回归，用的方法是最小二乘法，用法是：

b=regress(Y,X)

其中Y，X为按式（9.4.5）排列的数据，b为回归系数估计值.

[b,bint,r,rint,stats]=regress(Y,X,alpha)

这里Y，X同上，alpha为显著性水平（缺省时设定为0.05），b，bint为回归系数估计值和它们的置信区间，r，rint为残差（向量）及其置信区间，stats是用于检验回归模型的统计量，有三个数值，第一个是R2见式（9.4.16），第二个是F见式（9.4.15），第3个是与F对应的概率P，P＜α拒绝H0，回归模型成立.

残差及其置信区间可以用rcoplot（r，rint）画图.

例1 合金的强度y与其中的碳含量x有比较密切的关系，今从生产中收集了一批数据见表9-36.

表9-36 数据

试先拟合一个函数y（x），再用回归分析对它进行检验.

解 先画出散点图：

可知y与x大致上为线性关系.

设回归模型为

用regress和rcoplot编程如下：

得到

即的置信区间是[18.6851，36.2594]，的置信区间是[75.7755，199.2245]；R2=0.7985，F=27.7469，P=0.0012.

可知模型式（9.4.21）成立.

观察命令rcoplot（r，rint）所画的残差分布，除第8个数据外其余残差的置信区间均包含零点，第8个点应视为异常点，将其剔除后重新计算，可得

应该用修改后的这个结果.

例2 某厂生产的一种电器的销售量y与竞争对手的价格x1和本厂的价格x2有关.表9-37是该商品在10个城市的销售记录.

表9-37 销售记录(www.xing528.com)

试根据这些数据建立y与x1和x2的关系式，对得到的模型和系数进行检验.若某市本厂产品售价160（元），竞争对手售价170（元），预测商品在该市的销售量.

解 分别画出y关于x1和y关于x2的散点图，可以看出y与x2有较明显的线性关系，而y与x1之间的关系则难以确定，我们将作几种尝试，用统计分析决定优劣.

设回归模型为

编写如下程序：

得到但取α=0.01则模型不能用；R2=0.6527较小；

可以看出结果不是太好：P=0.0247，取α=0.05时回归模型式（9.4.22）可用，的置信区间包含了零点.下面将试图用x1，x2的二次函数改进它.

9.多项式回归

如果从数据的散点图上发现y与x呈较明显的二次（或高次）函数关系，或者用线性模型式（9.4.1）的效果不太好，就可以选用多项式回归.

（1）一元多项式回归，一元多项式回归可用命令polyfit实现.

例3 将17至29岁的运动员每两岁一组分为7组，每组两人测量其旋转定向能力，以考察年龄对这种运动能力的影响.现得到一组数据见表9-38.

表9-38 运动能力

试建立二者之间的关系.

解 数据的散点图明显地呈现两端低中间高的形状，所以应拟合一条二次曲线.

选用二次模型

编写如下程序：

得到

上面的s是一个数据结构，用于计算其他函数的计算，如

得到y的拟合值，及预测值y的置信区间半径delta.

用polytool（x0，y0，2），可以得到一个如图9-4的交互式画面，在画面中绿色曲线为拟合曲线，它两侧的红线是y的置信区间.你可以用鼠标移动图中的十字线来改变图下方的x值，也可以在窗口内输入，左边就给出y的预测值及其置信区间.通过左下方的Export下拉式菜单，可以输出回归系数等.这个命令的用法与下面将介绍的rstool相似.

图9-4 交互式拟合

（2）多元二项式回归，统计工具箱提供了一个作多元二项式回归的命令rstool，它也产生一个交互式画面，并输出有关信息，用法是

其中输入数据x，y分别为n×m矩阵和n维向量，alpha为显著性水平α（缺省时设定为0.05），model由下列4个模型中选择1个（用字符串输入，缺省时设定为线性模型）：

linear（线性）：y=β0+β1x1+…+βmxm

purequadratic（纯二次）：

interaction（交叉）：

quadratic（完全二次）

我们再作一遍例2商品销售量与价格问题，选择纯二次模型，即

编程如下：

得到一个如图9-5所示的交互式画面，左边是x1（=151）固定时的曲线y（x1）及其置信区间，右边是x2（=188）固定时的曲线y（x2）及其置信区间.用鼠标移动图中的十字线，或在图下方窗口内输入，可改变x1，x2图左边给出y的预测值及其置信区间，就用这种画面可以回答例2提出的“若某市本厂产品售价160（元），竞争对手售价170（元），预测该市的销售量”问题.

图9-5 vstool交互式拟合

图的左下方有两个下拉式菜单，一个菜单Export用以向MATLAB工作区传送数据，包括beta（回归系数），rmse（剩余标准差），residuals（残差）.模型式（9.4.24）的回归系数和剩余标准差为

另一个菜单model用以在上述4个模型中选择，你可以比较以下它们的剩余标准差，会发现以模型式（9.4.24）的rmse=16.6436最小.

10.非线性回归和逐步回归

本节介绍怎样用MATLAB统计工具箱实现非线性回归和逐步回归.

（1）非线性回归，非线性回归是指因变量y对回归系数β1，…，βm（而不是自变量）是非线性的.MATLAB统计工具箱中的nlinfit，nlparci，nlpredci，nlintool，不仅给出拟合的回归系数，而且可以给出它的置信区间，及预测值和置信区间等.下面通过例题说明这些命令的用法.

例4 在研究化学动力学反应过程中，建立了一个反应速度和反应物含量的数学模型，形式为

其中β1，…，β5是未知的参数，x1，x2，x3是三种反应物（氢，n戊烷，异构戊烷）的含量，y是反应速度.今测得一组数据见表9-39，试由此确定参数β1，…，β5，并给出其置信区间.β1，…，β5的参考值为（0.1，0.05，0.02，1，2）.

表9-39 数据

解 首先，以回归系数和自变量为输入变量，将要拟合的模型写成函数文件huaxue.m：

然后，用nlinfit计算回归系数，用nlparci计算回归系数的置信区间，用nlpredci计算预测值及其置信区间，编程如下：

用nlintool得到一个交互式画面，左下方的Export可向工作区传送数据，如剩余标准差等.使用命令

可看到画面，并传出剩余标准差rmse=0.1933.

（2）逐步回归，实际问题中影响因变量的因素可能很多，我们希望从中挑选出影响显著的自变量来建立回归模型，这就涉及到变量选择的问题，逐步回归是一种从众多变量中有效地选择重要变量的方法.以下只讨论线性回归模型式（9.4.1）的情况.

变量选择的标准，简单地说就是所有对因变量影响显著的变量都应选入模型，而影响不显著的变量都不应选入模型，从便于应用的角度应使模型中变量个数尽可能少.

若候选的自变量集合为S={x1，…，xm}，从中选出一个子集S1⊂S，设S1中有l个自变量（l=1，…，m），由S1和因变量y构造的回归模型的误差平方和为Q，则模型的剩余标准差的平方，n为数据样本容量.所选子集S1应使s尽量小，通常回归模型中包含的自变量越多，误差平方和Q越小，但若模型中包含有对y影响很小的变量，那么Q不会由于包含这些变量在内而减少多少，却因l的增加可能使s反而增大，同时这些对y影响不显著的变量也会影响模型的稳定性，因此可将剩余标准差s最小作为衡量变量选择的一个数量标准.

逐步回归是实现变量选择的一种方法，基本思路为，先确定一初始子集，然后每次从子集外影响显著的变量中引入一个对y影响最大的，再对原来子集中的变量进行检验，从变得不显著的变量中剔除一个影响最小的，直到不能引入和剔除为止.使用逐步回归有两点值得注意，一是要适当地选定引入变量的显著性水平αin和剔除变量的显著性水平αout，显然，αin越大，引入的变量越多；αout越大，剔除的变量越少.二是由于各个变量之间的相关性，一个新的变量引入后，会使原来认为显著的某个变量变得不显著，从而被剔除，所以在最初选择变量时应尽量选择相互独立性强的那些.

在MATLAB统计工具箱中用作逐步回归的是命令stepwise，它提供了一个交互式画面，通过这个工具你可以自由地选择变量，进行统计分析，其通常用法是：

其中x是自变量数据，y是因变量数据，分别为n×m和n×1矩阵，inmodel是矩阵x的列数的指标，给出初始模型中包括的子集（缺省时设定为全部自变量），alpha为显著性水平.

stepwise命令产生三个图形窗口：StepwiseTable，Stepwise History，StepwisePlot.

Stepwise Table窗口中列出了一个统计表，包括回归系数及其置信区间，模型的统计量（RMSE R-square，F，p等，其含义与regress，rstool相同）.你可以通过这些统计量的变化来确定模型.

StepwiseHistory窗口显示RMSE的值及其置信区间.

StepwisePlot窗口，显示回归系数及其置信区间，绿色表明在模型中的变量，红色表明从模型中移去的变量，两边有虚线或实线，虚线表示该变量的拟合系数与零无显著差异，实线则表明有显著差异.在这个窗口中还有ScaleInputs和Export按钮.

按下ScaleInputs表明对于输入数据的每列进行正态化处理，使其标准差为1.点击Export产生一个菜单，表明了要传送给MATLAB工作区的参数，它们给出了统计计算的一些结果.

下面通过一个例子说明stepwise的用法.

例5 水泥凝固时放出的热量y与水泥中4种化学成分x1，x2，x3，x4有关，今测得一组数据如下，试用逐步回归来确定一个线性模型

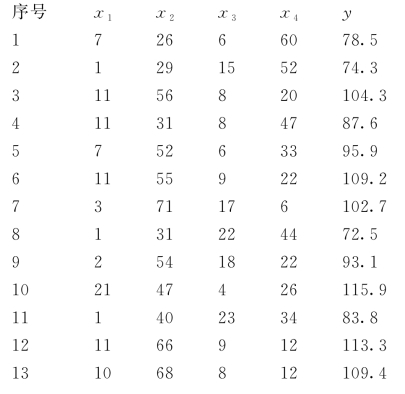
编写程序如下：

得到StepwiseTable如下：

可以看出，x3，x4不显著，移去这两个变量（程序为stepwise（x，y，[1，2]））后的统计结果如下：

这个表中的x3，x4两行用红色显示，表明它们已移去.

从新的统计结果可以看出，虽然剩余标准差s（RMSE）没有太大的变化，但是统计量F的值明显增大，因此新的回归模型更好一些.使用前面的回归分析方法可以求出最终的模型为

y=52.5773+1.4683x1+0.6623x2.

用事件概率预测未来