使用OLS估计的Logit模型参数及其检验

（一）Logit模型基本概念

1.Logit回归总体回归模型与总体回归函数

Logit模型也称为对数单位模型，是利用逻辑斯蒂分布作为u*i的分布构建的二元离散选择模型，假设：

其中，Y*、X、β、u*的形式与多元回归模型相同。随机扰动项满足相互独立假定且服从逻辑分布；二元离散被解释变量Y假定满足：

那么，因为逻辑分布的密度函数为，那么，分子分母同时乘上e-2X可得，因此，逻辑分布的密度函数是一个对称分布，故此有P（u*＞-Xβ）=P（u*＜Xβ）。由，可得总体回归模型为

式（7-44）称为Logit模型。总体回归函数即为

总体回归函数E（Y）具有下列特征：

1）当Xβ→+∞时，E（Y）=P（Y=1）→1，反之，当Xβ→-∞时，E（Y）=P（Y=1）→0；当Xβ=0时，E（Y）=P（Y=1）=0.5，因此，模型（7-45）可保证样本回归方程的观测值位于[ 0，1]内。

2）存在一个拐点，在拐点之前，E（Y）=P（Y=1）随着Xβ增大增长速度越来越快，在拐点之后增长速度越来越慢，并逐渐趋向于1。

2.机会比率

由可得：，称：

为机会比率（odds），机会比率表明了在样本点中同一个点Xi上，事件Y=1发生的概率是事件Y=0发生概率eXiβ倍。

3.优势比

在样本点Xi上的机会比率为odds1，在样本点Xj上的机会比率为odds2，称两个机会

比率的比值为优势比（odds Ratio，简称OR），即

若P1＞P2，则

若P1＜P2，则

若P1=P2，则

显然，OR是否大于1可以用作两种情形下发生概率大小的比较。

4.对数单位

称机会比率的自然对数为对数单位，易知：

可见，对数单位是解释变量X和参数β的线性函数。式（7-48）也称为Logit模型。式（7-48）和式（7-45）本质上是相同的，Logit模型有以下特点。

1）随着P（Y=1）从0变化到1，对数单位从-∞变化到+∞，这就保证了P（Y=1）不会因为解释变量X的变化而越出[0，1]。

2）虽然对数单位是解释变量X的线性函数，但P（Y=1）=并不是解释变量X的线性函数，这是Logit模型与线性概率模型的最大区别。

3）Logit模型中参数的直观含义是在保持其他因素不变的情况下，Xi变动一个单位，对数单位平均变动βi个单位，但是二元离散选择模型更关注的是随Xi

变动，P（Y=1）的变动情况。保持其他因素不变的情况下，Xi变动一个单位，Xβ变动βi个单位，那么变动前后优势比

4）如果设法估计出β的估计值，则可以直接计算出给定条件X=X*下P（Y=1）的估计值

（二）Logit模型的估计

如果对式（7-48）直接进行估计，那么当事件发生时，P（Y=1） =1，，当事件没有发生时，P（Y=1）=0，，机会比率的对数都没有意义，因此，如果仅有个体数据，则无法直接利用普通最小二乘法进行参数估计，只能采用极大似然法。下面简单讨论分组数据和未分组数据情况下Logit模型的估计模型的估计思路。

1.分组数据的参数估计

在对式（7-48）进行估计时，无法直接观测，解决办法是通过对样本点进行分组，利用每一组内的被解释变量取1的相对频率作为P（Y=1）的估计，然后利用普通最小二乘法进行参数估计。下面通过一个例子进行说明（如表7-9所示）。

表7-9　高中毕业生的家庭收入（Xi）与上大学（Yi）群组相关数据

续表

此样本点共包含355个个体，按照家庭收入水平共分为10组，每一组内的个体个数为Ni，上大学（Yi=1）的个体个数为ni，由此可以估计出每一收入水平Xi下pi的估计值；如果每一组的Ni足够大，依据统计学中的大数定律，依 概率收敛向pi。利用可 以使用OLS估计Logit模型（7-48）。

现在面临的问题是，如果利用式（7-49）形式的总体回归函数，总体回归模型表现为

总体回归模型的个别值形式为，在分组Xi中，Yi服从二项分布，那么εi也将服从二项分布，如果Ni足够大，利用中心极限定理，随机扰动项近似服从：εi～，显然，类似于线性概率模型，Logit模型（7-48）的随机扰动项的方差取决于pi，因此，也存在异方差，可以通过作为权重，进行WLS估计。

2.未分组数据的参数估计

对于未分组的数据，只能采用极大似然法进行参数估计。假设样本容量为n，对于样本点中的第i个点（Yi，Xi）来讲，记Pi=P（Yi=1/X=Xi），在给定X=Xi的条件下，被解释变量Y取0或1的概率分别为1-Pi、Pi，这就意味着在X=Xi条件下，Y的条件分布为P（Y）=pYi（1-pi）1-Y，Y=0、1，考虑到重置抽样后样本点内各个点代表的事件之间的独立性，那么样本点代表的事件发生的概率为，那么似然函数为

对数似然函数为

利用微积分知识，通过求便可得到β的极大似然估计量。

Logit模型参数的极大似然估计量满足一致性、渐进有效性和渐进正态性，关于Logit模型的相关检验已超出本书范围，下面仅通过一个例子说明Logit模型的参数估计和期望-预测表检验。

例7-3 为探索居民家用轿车购买决策的影响因素，考虑家庭年收入X1（万元）、户主年龄X2（岁）两个因素，轿车购买状态用虚拟变量Y表示，定义Y的取值规则为

变量测量结果见表7-10，现运用Logit模型进行居民家用轿车购买决策影响因素分析。

表7-10　变量测量结果

估计结果见表7-11。

表7-11　样本回归方程估计结果

由表7-11可见，样本回归方程为

下面通过期望-预测表检验对估计结果进行简单评价，截断值设为0.5，这就意味着如果≥0.5，相应的预测值为1，如果＜0.5，则相应的预测值为0。

表7-12　期望-预测表检验结果(www.xing528.com)

从表7-12可见，被解释变量取值为0的20个个体，预测准确的有19个，正确率95%，被解释变量取值为1的22个个体，预测准确的有21个，正确率为95.45%，总体正确率95.24%，说明模型整体拟合效果较好。

（三）Probit模型

类似于Logit模型，在Probit模型是利用标准正态分布作为u*i的分布构建的二元离散选择模型，式（7-43）中的F（.）为标准正态分布的分布函数，那么

E（Y）=P（Y=1）=P（Y*＞0）=P（u*＞-Xβ）=P（u*＜Xβ）==Φ（Xβ）这就意味着总体回归函数为

总体回归模型为

Probit模型总体回归函数的特征与Logit模型模型总体回归函数函数性质十分相似，logit曲线比正态分布尾部更厚，两条曲线都是在p=0.5处有拐点，logit曲线更接近t（7）（格林认为是t（4））。所以，对于Xβ的中间值（比如-1.2到1.2）来说，两类分布给出的结果类似，但是当Xβ非常小时，逻辑斯蒂回归模型比Probit回归模型倾向于给出Y=0（y*≤0）较大的概率值，而在Xβ非常大时，倾向于给出Y=0（y*≤0）较小的概率值。

表7-13　Probit模型和logit模型概率值

对于采用重置抽样的方法，抽取到的样本容量为n的样本点，似然函数仍为L（β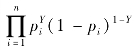）=，对数似然函数为

通过求，便可得到β的极大似然估计量。

由E（Y）=Φ（Xβ）=Φ（β1+X2β2+…+X1βk）可知：

其中，f（.）表示正态分布的密度函数，这就意味着保持其他条件不变，当某一个解释变量Xi变化一个单位时，P（Y=1）变化f（β1+X2β2+…+Xkβk）βi个单位。

下面对例题7-3采用Probit模型进行估计，结果见表7-14。

表7-14　样本回归方程估计结果

由表7-14可知样本回归方程为，期望-预测表检验结果见表7-15。

表7-15　期望-预测表检验结果

由表7-15可见，利用Probit模型对该问题进行参数估计，被解释变量为0和1的两部分预测准确率以及整体预测准确率与利用logit模型预测的准确率相同，也能够对该问题进行较好的拟合。

表7-16　Logit模型和Probit模型的拟合值与预测值

续表

由表7-16可见，Logit模型和Probit模型预测结果完全相同，但是对于较大的概率，Probit拟合值整体上大于Logit模型模型拟合值，对于较小的概率Probit模型的拟合值整体上小于Logit模型模型拟合值，说明Probit模型的条件概率以更快的速度趋向0和1。

练习题

1.为了评价从1979年7月起联邦放宽利率管制政策以来的影响，S.兰格对1975年第三季度至1983年第二季度十七数据估计得到如下模型：

其中Y为3个月国库券利率；P为预期通货膨胀率；Un为季节调整后的失业率；M为基础货币的变化；D虚拟变量，对从1979年7月1日开始的观测值取1。

试回答：

a.对估计结果进行解释；

b.放宽利率管制有何效果？

2.有如下分段线性回归模型：Yi=α1+β1 Xi+β2（Xi-X*）Di+μi，其中Y为销售佣金；X为销售员的销售额；X*销售额的门槛值；D为虚拟变量，。现假设在X*处，如图7-7所示，不但有斜率系数的一个变化，而且有回归线的一个跳跃，你该如何修改原计量经济模型？

图7-7　一类特殊的总体回归线

3.根据美国2000年第一季度至2016年第二季度的数据，我们得到了如下的咖啡需求函数的回归方程：

其中，Q=人均咖啡消费量（单位：磅）；P=咖啡的价格（以1967年价格为不变价格）；I=人均可支配收入（单位：千元，以2000年价格为不变价格），P*=茶的价格（1/4磅，以2000年价格为不变价格）；T=时间趋势变量（2000年第一季度为1，……，2016年第二季度为66）；D1=1：第一季度；D2=1：第二季度；D3=1：第三季度。

请回答以下问题：

（1）模型中P、I和P*的系数的经济含义是什么？

（2）咖啡的需求是否富有弹性？

（3）咖啡和茶是互补品还是替代品？

（4）如何解释时间变量T的系数？

（5）如何解释模型中虚拟变量的作用？

（6）哪一个虚拟变量在统计上是显著的？

（7）咖啡的需求是否存在季节效应？

4.一个由容量为209的样本估计的解释CEO薪水的方程为

其中，Y表示年薪水平（单位：万元），X1表示年销售收入（单位：万元），X2表示公司股票收益（单位：万元），D1，D2，D3均为虚拟变量，分别表示金融业、消费品行业、公用事业。假定对比行业为交通运输业。

（1）解释三个虚拟变量参数的经济含义。

（2）保持X1和X2不变，计算公用事业和交通运输业之间估计薪水的近似百分比差异。

这个差异在1%的显著性水平上是统计显著的吗？

（3）消费品行业和金融业之间的估计薪水的近似百分比差异是多少？写出一个使你能直接检验这个差异是否统计显著的方程。

5.试在家庭对某商品的消费需求函数Y=α+βX+μ中以加法形式引入虚拟变量，用以反映季节因素（淡、旺季）和收入层次差距（高、中、低）对消费需求的影响，并写出各类消费函数的具体形式。

6.假设利率r＜0.08时，投资I取决于利润X；而利率r≥0.08时，投资I同时取决于利润X和一个固定的级差利润R。试用一个可以检验的模型来表达上述关系，并简述如何对利率的影响进行检验。

【注释】

[1]本节可作为本科生授课过程中的选讲内容。