统计假设检验：方法与错误

假设检验的全称为统计假设检验，它是统计推断的重要问题之一。顾名思义，假设检验分成两部分内容，先做出一个假设，然后用数据和统计的办法去检验这个假设是否成立，就是要做出“接受”还是“拒绝”这个假设的判断。常用方法有μ检验、t检验、κ2检验、F检验和置换检验等。置换检验称为是非参数检验，而其他的均属于参数检验，这个概念的意思我们随后解释。

我们在这一小节叙述假设检验的一般过程，在以后各小节中结合例子来说明怎样用统计方法来完成假设检验。

（1）建立假设

继续前例，从A、B两个班级各抽取5名学生来测试班级的数学水平，在测试前教师估计A班的5名同学的平均成绩，这就是一个假设，通常记成

在假设检验中，我们会给出与H0对立的假设H1，例如在这个问题中假设

在这两个假设中，称H0是“零假设”，它常常是我们希望成立的一个假设；称H1是“备选假设”。

根据零假设和备选假设的关系，可以将假设分成三类。设需要检验的统计量是θ，那么：

H0：θ＝θ0，H1：θ≠θ0；

H0：θ≤θ0，H1：θ＞θ0；

H0：θ≥θ0，H1：θ＜θ0。

第一种称双侧检验问题，因为H1在H0的两侧；第二种称右侧检验问题，因为H1在H0的右侧；相应地第三种称为左侧检验问题。注意在后两种假设中，H0的等号可以移到H1中，例如第二个可以是H0：θ＜θ0，H1：θ≥θ0，它依然称为右侧检验。

（2）选择统计量

我们再次回到A、B两个班级各抽取5名学生来测试班级的数学水平的例子。如果要比较哪个班级数学成绩好一点，可以有几种不同的比较方法。例如可以比较θ＝x1-y1，将最优秀的学生比，看看哪个班级更好一些；也可以比较θ＝x5-y5，比较最差的学生；还可以比较这5个同学的平均成绩，即取θ＝x--y-。这些x1-y1，x5-y5和x--y-称为检验的统计量。这个例子说明，即使目的相同，都是为了比较两个班级的数学水平，但是可以选取不同的检验统计量。

如果统计量已经选定，我们能不能做如下的假设呢？

H0：θ＞0；H1：θ≤0

思考：如果H0表示A班成绩好，那么用语言叙述H1的含义是什么？

我们已知为A班与B班比较的检验统计量，所以按上节内容以此类推可得出：

当θ＝0时，则推断A、B两班数学水平相当；当θ＜0时，则A班数学成绩比B班差。

设X1，X2，…，Xn是从同一个总体、独立地抽取的样本，这里所谓的独立，是指前面k次的抽取不会影响第k＋1次的抽取结果。例如一个袋子里装有编号是1和2的两个球，两人去摸球，甲先摸而摸到后不放回，然后乙摸，这两个人的摸球结果都是随机变量，但是它们不是独立的，因为先摸的结果会直接影响后摸的结果；然而采用放回摸球，就是甲先摸而摸到后放回，然后乙摸，则是独立的。一般袋子里有n个球，m个人不放回摸球，当n／m＞10时可以近似地认为是独立的。

最常用的统计量有样本均值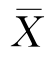

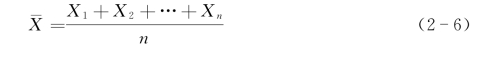
样本标准差S

(www.xing528.com)

思考：为什么在样本标准差的定义式中的分母用n-1而不是n？

这乍一看确实是个非常违背常理的点，但是这个小小的n-1却能使我们得出的数值更加准确。这是为什么呢？我们进行一个相对简单的推导过程。

假设我们已知随机变量X的数学期望μ，然而方差S 2未知，那么根据方差公式可得：

注意此时公式中的分母为n，这也是符合我们的直觉的。

那么现在我们回到实际情况：数学期望μ未知。这时，我们倾向直接将样本均值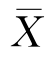替代上面公式μ的。但是这样做的话，得出的方差将低于实际方差。因为：

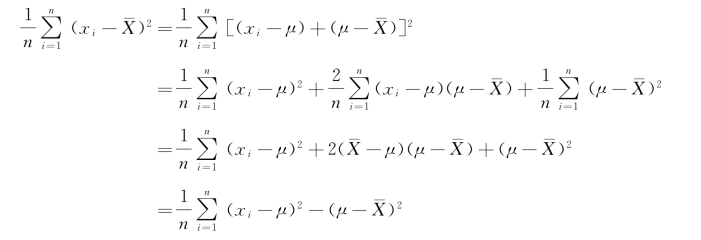
于是我们发现，分解出来与数学期望μ建立关系时，后面永远要减去一个大于等于0的值。只有当时，，继而。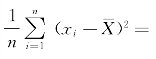

换言之，除非，否则永远

即在分母为样本数n的情况下，样本方差（标准差）永远小于实际情况！

那么如何解决这个问题呢？那就是把样本方差公式中的分母改成n-1，将偏小的树枝稍微“放大”，就能获得相对正确的估计值了。

（3）设置显著性水平

我们还需要设置一个显著性水平。那么显著性水平是什么？为什么要有显著性水平？这就要从头开始说起了。

假设检验是从总体中随机抽取一个样本，然后对样本计算检验统计量，根据计算结果判断是否接受零假设。这种推断基于一个假设，那就是抽取的样本能够完全代表总体。但是实际上这是不可能的，由于样本的随机性，样本只能趋近于总体而不可能完全等于总体，这就表示样本所得出的检验结果有可能与实际情况不符，并且只要我们抽取样本，这种错误就不可避免。

假设检验可能犯的错误有两种。

一是抽样检验的结果显示H0不成立，即结论不支持零假设，而实际上零假设是正确的。这是“该接受的未接受”错误，称为第一类错误。发生第一类错误的概率称为拒真概率，通常记为α。

二是统计检验的结果支持H0，而实际情况却零假设不成立。这是“不该接受的被接受”的错误，称为第二类错误，其发生的概率称为取伪概率，通常记为β。

理论研究表明，当样本量固定时，α与β必此消彼长，只有在样本量增大时α和β才同时减小，所以通常的做法是将拒真概率α控制在特定水平上。一般将α称为显著性水平，这里稍微分析一下显著性水平α的意义。用μ0和μ分别表示总体和采样的均值，那么μ是依赖于采样的随机变量。假设H0：θ＝μ-μ0＝0，就是总体均值与样本均值一样。由于μ是随机变量，要求H0成立未必太过苛刻，因此我们假设一个常数δ＞0，当θ∈［-δ，δ］时，就认为H0成立。这个区间［-δ，δ］称为这个假设的置信区间或者接受域，而（-∞，-δ）∪（δ，∞）称为这个假设的拒绝域。第一类错误就是μ错误地落在拒绝域了。因此可以将α取成

第一个式子就是μ落在置信区间外的概率。因为显著性水平是个概率，因此不少教材会用p来表示显著性水平，并且通常规定p＝0.05或0.01，意思是我们允许样本检验结果产生第一类错误的概率为0.05%或0.01%及以下。读者从图2-32可以看出，对于正态分布来讲，取p＝0.05就是指|μ-μ0|＞2σ，而取p＝0.01就是指|μ-μ0|＞3σ，所以犯第一类错误的概率相当低。

事实上对于一个具体问题如何选择一个合适的显著性水平（通常称p值）是一个很复杂的问题，是很多研究的焦点。

（4）计算检验统计量并做出判断

这一步已经没有什么问题了。我们先确定检验统计量属于什么分布，根据显著性水平，确定接受域，计算检验统计量，看看是在接受域还是不在接受域，然后决定是否接受零假设。