例1(续8.1节例1) 定性考察反映高等教育发展状况的五个方面十项评价指标,可以看出,某些指标之间可能存在较强的相关性,如果直接用这些指标进行综合评价,必然造成信息的重叠,影响评价结果的客观性。我们的问题是,能不能把这个数据的10个变量用一两个综合变量来表示?综合变量又包含多少原始信息、怎么解释并应用综合变量对学生排序?
主成分分析方法可以把多个指标转化为少数几个不相关的综合指标,因此,可以考虑利用主成分进行综合评价。利用MATLAB软件对十个评价指标进行主成分分析,相关系数矩阵的前几个特征根及其贡献率见表8.3.1。可以看出,前两个特征根的累计贡献率已达到90%以上,主成分分析效果很好。
表8.3.1 解释的总方差
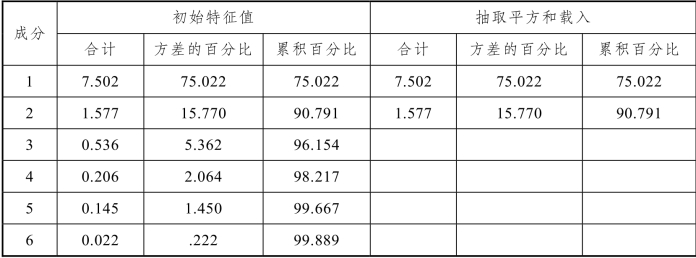
下面选取前两个主成分(累计贡献率达到90.791%)进行综合评价。前两个特征根对应的特征向量见表8.3.2。
标准化变量的前两个主成分对应的特征向量见表8.3.3。
由此可得前两个主成分分别为

表8.3.2 成分矩阵

表8.3.3 成分矩阵

从主成分的系数可以看出,第一主成分主要反映了前六个指标(学校数、学生数和教师数方面)的信息,第二主成分主要反映了高校规模和教师中高级职称的比例。把各地区原始十个指标的标准化数据代入表达式,就可以得到各地区的这两个主成分值,并可以据此排序。可以看出,各地区高等教育发展水平存在较大的差异,高教资源的地区分布很不均衡。北京、上海、天津等地区高等教育发展水平遥遥领先,陕西和东北三省高等教育发展水平也比较高。贵州、广西、河南、安徽等地区高等教育发展水平比较落后。
MATLAB程序如下:

MATLAB中与主成分分析有关的几个函数:
求协方差矩阵cov(X)或cov(x, y);
计算特征值和特征向量e=eig(a),得到的e是一个包含矩阵a的特征值的矢量;[v,d]=eig(a),得到的d为对角阵,其对角元为a的特征值,且将特征值按由小到大的次序排列;v是一个与矩阵a阶数相同的方阵,它的每一列是矩阵a的一个特征值所对应的特征向量。v的第j列与d的第j个对角元相对应。
进行主成分分析用princomp( )函数。
SPSS中进行主成分分析的过程:
(1)在SPSS中,打开对应数据文件,依图8.3.2所示点击菜单“分析→降维→因子分析”(SPSS中,主成分分析和因子分析属于同一个总选项,操作界面相同,只是选项有所不同),出现“因子分析”对话框(见图8.3.3)。

图8.3.2 SPSS因子分析菜单
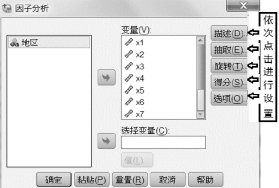
图8.3.3 SPSS因子分析菜单设置
(2)选择参与因子分析的变量。(https://www.xing528.com)
①“变量”框:选取参与因子分析的变量。这里选择X1到X10。选取不同的变量,结果是不一样的。
②“选择变量”框:如果空置,全部参与数据因子分析;如果选择该项,则根据选择变量的给定值来筛选参加因子分析的数据。
下面对图8.3.3右侧的按钮进行重点说明:
(3)单击“描述”按钮,可输出描述统计量和初始分析结果。

图8.3.4 因子分析菜单设置
(4)单击“抽取”按钮,系统弹出图8.3.4(a),因子分析有关控制参数设置:因子提取方法,默认的是主成分,即进行主成分分析;如果不选主成分,对于因子分析,点击下拉菜单倒三角 ,出现多种方法供选择,可以根据实际情况选择一种方法。
,出现多种方法供选择,可以根据实际情况选择一种方法。
碎石图是特征值(方差)的图像表示,可以直观地给出特征值的大小。
提取因子数,默认的是特征值大于1,若想输出所有的因子,填0,也可以直接填上要提取的因子个数。
(5)单击“旋转”按钮,弹出图8.3.4(b),选择旋转方法:主成分分析选默认的“无”,如果是因子分析,根据实际情况选择(如后面对例1继续进行因子分析时,选择最大方差法)。
载荷图可以直观地反映选取的主成分(或因子)与原始变量的相关性。
(6)单击“得分”按钮,弹出图8.3.4(c),选择将因子得分“保存为变量”时,会在数据集上,添加新变量FAC1_1、FAC2_1、……来保存因子得分,可以根据因子得分进行排序。
完成所有设置后,单击“OK”按钮,便可输出系列结果。
这个数据集的点是10维的,每个观测值可看成是10维空间中的一个点。这里的初始特征值initial eigenvalues就是10维空间椭球的10个主轴长度,又称特征值(是数据相关矩阵的特征值),最大的有7.502 159,占所有特征值总和(又叫总方差)的75.021 586%[=7.502159(7.502159 +1.577 +0.536 +0.206 +0.145 +0.022+…)]。
前两个主成分的特征值累积占总方差的90.791 458%(=75.021 586%+15.769 872%),后面的特征值的贡献越来越少,这里,选前两个主成分即可。碎石图(见图8.3.5,特征值的图示、连线的陡峭程度直观地展示了特征值变化的大小)直观地展示了这一点。
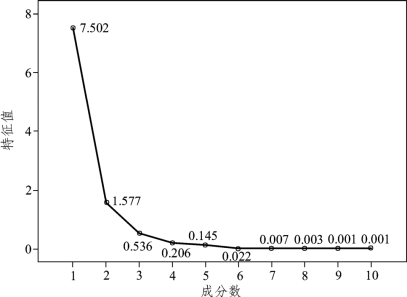
图8.3.5 10个成分的特征值的碎石图
主成分是原数据10个变量的线性组合。前两个主成分具体怎么表达呢?SPSS输出成分矩阵表(Component Matrix),见表8.3.4、表8.3.5。
表8.3.4 成分矩阵
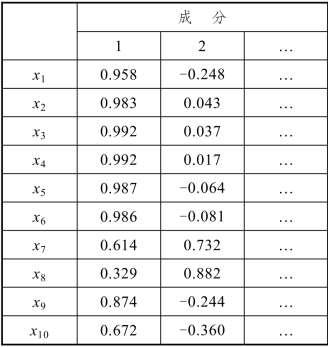
表8.3.5 成分得分系数矩阵
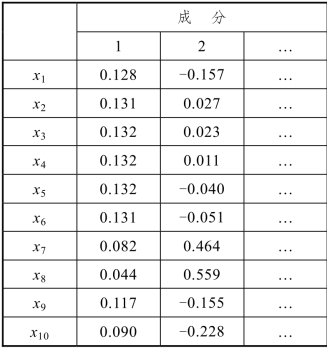
表8.3.4的每一列代表一个主成分作为原来变量线性组合的系数,系数称为主成分载荷,它表示主成分和原始变量的线性相关系数。它分别是数据相关阵的各个特征值所相应的特征向量,这里它不是单位向量,而是单位特征向量乘以相应特征值的平方根(称为载荷)。载荷为对应的主成分(因子)和原变量的相关系数,这也是单位特征向量乘以相应特征值的平方根的原因。相关系数(绝对值)越大,主成分对该变量的代表性也越大。这里,第一主成分对各个变量解释得都很充分(相关系数(绝对值)都比较大),而其后的主成分则不然。
为了更直观地解释主成分所代表的意义,把第一和第二主成分对应的载荷配对,画出载荷图(loading plot),直观地显示了如何解释原始变量。
新增变量FAC1_1、FAC2_1的值,即因子得分是如何计算出来的?它们等于表8.3.5中成分得分系数和对应变量标准化后值的乘积之和。这里,标准化的具体计算:如某变量的均值74.98,样本标准差9.688,则65对应的标准化后的值为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




