高职应用数学：随机事件概率

9.1.2.1 概率与频率的概念

对于随机试验中的随机事件，在一次试验中是否发生，虽然不能预先知道，但是它们在一次试验中发生的可能性是有大小之分的.比如掷一枚均匀的硬币，那么随机事件A（正面朝上）和随机事件B（正面朝下）发生的可能性是一样的（都为）.又如袋中有8个白球，2个黑球，从中任取一球.当然取到白球的可能性要大于取道黑球的可能性.一般地，对于任何一个随机事件都可以找到一个数值与之对应，该数值作为发生的可能性大小的度量.

定义1

随机事件A发生的可能性大小的度量（数值），称为A发生的概率，记为P（A）.

对于一个随机试验来说，它发生可能性大小的度量是自身决定的，并且是客观存在的.概率是随机事件发生可能性大小的度量是自身的属性.一个根本问题是，对于一个给定的随机事件发生可能性大小的度量——概率，究竟有多大呢？

再来看，掷硬币的试验，做一次试验，事件A（正面朝上）是否发生是不确定的，然而这是问题的一个方面，当试验大量重复做的时候，事件A发生的次数，也称为频数，体现出一定的规律性，约占总试验次数的一半，也可写成

一般的，设随机事件A在n次试验中出现nA次，比值称为事件A在这n次试验中出现的频率.历史上有人做过掷硬币的试验.见表9-2.

表9-2 掷硬币的试验

从表9-2可以看到，不管什么人去抛，当试验次数逐渐增多时，fn（A）总是在0.5附近摆动而逐渐稳定于0.5.从这个例子可以看出，一个随机试验的随机事件A，在n次试验中出现的频率fn（A），当试验的次数n逐渐增多时，它在一个常数附近摆动，而逐渐稳定与这个常数.这个常数是客观存在的，“频率稳定性”的性质，不断地为人类的实践活动所证实，它揭示了隐藏在随机现象中的规律性.

9.1.2.2 概率的性质

由于概率是频率的稳定值，因此频率具有的性质，概率也应有相应的性质：

（1）非负性：P（A）≥0；

（2）规范性：P（Ω）=1；

注意 性质2反过来不一定成立.就是说概率为1的事件不一定为必然事件.同样，概率为0的事件不一定为不可能事件，这方面的例子在下一章再举.

（3）有限可加性：若Ai∈F，i=1，2，3，…，n且AiAj=∅（i≠j），则，即有限个互不相容的事件的和事件的概率等于这些事件的概率之和.

因，从而有.

9.1.2.3 古典概型

本章我们讨论一类最简单的随机试验，它具有下述特征：

（1）样本空间的元素（基本事件）只有有限个，不妨设为n个，记为

ω1,ω2,…,ωn;

（2）每个基本事件出现的可能性是相等的，即有

P(ω1)=P(ω2)=…=P(ωn).

称这种数学模型为古典概型.

它在概率论中具有非常重要的地位，一方面它比较简单，既直观，又容易理解，另一方面它概括了许多实际内容，有很广泛的应用.

通过研究发现，在古典概型中，事件A的概率是一个分数，其分母是样本点（基本事件）总数n，而分子是事件A包含的基本事件数k.

例如：将一枚硬币连续掷两次就是这样的试验，也是古典概型，它有四个基本事件，（正、正），（正、反），（反、正），（反、反），每个基本事件出现的可能结果都是.

但将两枚硬币一起掷，这时试验的可能结果为（正、反），（反、反），（正、正）但它们出现的可能性却是不相同的，（正、反）出现的可能性为，而其他的两个事件的可能性为.(www.xing528.com)

它不是古典概型，对此历史上曾经有过争论，达朗贝尔曾误为这三种结果的出现是等可能的.

判别一个概率模型是否为古典概型，关键是看“等可能性”条件满不满足.而对此又通常根椐实际问题的某种对称性进行理论分析，而不是通过实验来判断.

由古典概型的计算公式可知，在古典概型中，若P（A）=1，则A=Ω.同样，若P（A）=0，则A=∅.

不难验证，古典概型具有非负性、规范性和有限可加性.

利用古典概型的公式计算事件的概率关键是要求基本事件总数和A的有利事件数，则需要利用数列和组合的有关知识，且有一定的技巧性.

例1 在盒子中有五个球（三个白球、二个黑球）从中任取两个.问取出的两个球都是白球的概率？一白、一黑的概率？

分析 说明它属于古典概型，从5个球中任取2个，共有种不同取法，可以将每一种取法作为一个样点.则样本点总数是有限的.由于摸球是随机的，因此样本点出现的可能性是相等的，因此这个问题是古典概型.

解 设A={取到的两个球都是白球}，B={取到的两个球一白一黑}

基本事件总数为.

A的有利事件数为.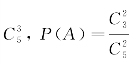

B的有利事件数为.

例2 一套五册的选集，随机地放到书架上，求各册书自左至右恰好成1，2，3，4，5的顺序的概率.

解 将五本书看成五个球，这就是一个摸球模型，基本事件总数5！

令A={各册自左向右或成自右向左恰好构成1，2，3，4，5顺序}

A包含的基本事件数为2，

∴.

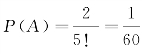例3 从52张扑克牌中取出13张牌来，问有5张黑桃、三张红心、3张方块、2张草花的概率是多少？

解 基本事件数为：.

令A表示13张牌中有5张黑桃、3张红心、3张方块、2张草花.

A包含的基本事件数为：.

∴.

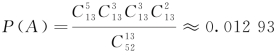课后提升

1.设汽车号牌由7位数组成，任取一个号码，求下列两个事件的概率：

（1）后三位数是123；（2）后三位各不相同.

2.现在有7名乒乓球队员，3名足球队员，从中任意抽出3个队员，求至少有一名足球队员的概率.

答案

1.(1)0.001;(2)0.72.

2..