新直线数量与比例因子、分形维数、层级构成等的关系

模块化架构不仅仅是一个能够保证系统所有组成部分有效并持续结合在一起的功能过程，也是一个能够促使系统有效运转的操作过程。例如，关系到城市经济运行的不同职能取决于人口是否能够达到一定数量，并且职能越是具体，需要维持的人口数量就越多。简而言之，越是细分的职能越需要获得规模经济，以便不同职能模块的规模和间隔可以在不同等级层次形成常规模式。这些职能模块继而会被复制，并根据其规模进行改变。

我们可以通过简单的几何来说明如何测量一个物理模块，并产生一个在所有尺度上都相似的分形。想象一下，为了在一条中间有障碍物的直道沿途设置栅栏，我们现在需要扩大空间。如果我们将这条道分成同样长度的三段，取其中两段，如图8.1a增加两段顶端相互接触的栅栏从而形成一个等边三角形，我们就可以绕开障碍物。但是，这就明显地将直线L的长度增加了一个单位（其原来的长度为三个单位），所以栅栏的新长度就变成了（4/3）L。如果我们继续将每一段细分成三段，重新安排中间一段的位置形成同样的等边三角形，我们就会进一步增加栅栏的长度，但是增加的幅度比原来要小。如果细分后的四段每段都再细分，那么栅栏长度就会在原来增加了4/3的基础上又增加4/3，也就是说新的栅栏长度就会变成（4/3）（4/3）L。我们可以不断在越来越小的尺度上继续细分，这样在第n层次栅栏的长度就会变成（4/3）nL。

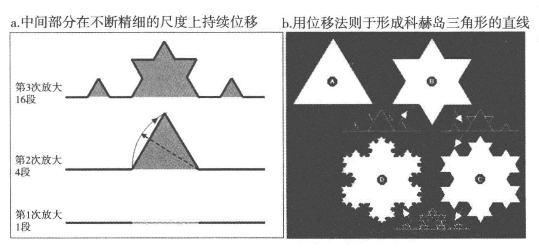
图8.1　构建空间填充曲线：科赫雪花曲线

我们现在将最初的栅栏定义为直线L（1），那么直线L（n）的长度就可以定义为

其中φ是复合标度比，在这个案例中为4/3。显然，我们可以改变这个比例。当这个比例达到2时，就意味着这条线充满了整个二维平面。这种架构就是在不同尺度上循环应用同一法则，然后产生一个自相似的模式，在这个案例中，自相似的模式就是每个尺度上都会出现一个三角形，这从某种程度上说就是这整个架构的标志。这个自下而上的结构产生了一种分形图形，即一种常规几何图形，其中包括了间断的，有时从统计学角度看并不规则的组成部分，这些部分在不同尺度上被重复，反映了一个被不断迭代的相同过程。这种模式内在包含一个等级体系，这一等级体系可以被抽象成如图8.2所示的树状图。

我们以上说明的这个迭代过程会产生很多奇怪的结果。首先，如果这种不断增加类似结构的过程无限循环下去，那么这条直线的长度就会变得无限长，但是很明显，由此产生的形状所包围住的区域，无论是在图8.1a的科赫曲线中还是在图8.lb的科赫岛（也称为科赫雪花）中，其面积都是一个固定的值。其次，如果这条直线变得越来越曲折，那么这条欧几里得维数为1的直线看起来就似乎有了平面的维数2。空间填充的理念可以被归纳在分形维度的思想里。阐释这一点的最好方法就是通过以下方程计算新直线N的数量：

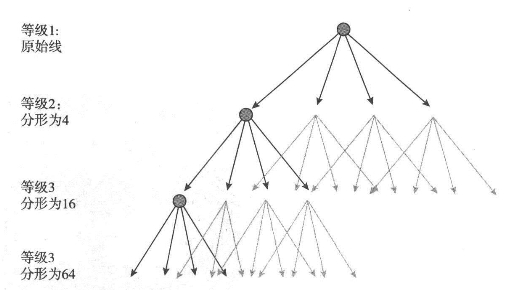
图8.2　构建分形图形时构成部分的等级层次

其中K为比例常数，可确保比例与背景相符，ε为比例因子，可按比例增加现有直线数量至下一次迭代，D为分形维数。事实上，对于图8.1中的定率分形，每次迭代比例都是固定的。

显然，在任何一个尺度上，分形维数都可以通过以下方程计算得出：(www.xing528.com)

如果我们假设K是一个统一的常数，那么我们就可以计算出一系列图形的分形维数，由此我们就可以得知代入比例因子ε得出的N为多少。在科赫曲线中，N=4且ε=1/3，因而D=log4/log3=1.2619。很容易看出，如果直线增加的速度小于比例因子，那么其维数就会保持为1，这也是直线的欧几里得空间维数，但是如果其速度为因子的两倍，也就是N=4且ε=1/2，那么维数就会等于2，这就是一条真正充满空间的曲线。如果我们在不同的尺度εk上，也就是在不同比例因子的情况下，有一系列数量为Nk且实证测量过的线段，那么我们就可以根据最小二乘法通过方程8.2计算出分形维数，如下

图8.la中的科赫曲线维数大约为1.26，而比这更曲折的曲线如峡湾海岸线，其维数大约为1.7。相对和缓的曲线，如澳大利亚南部的海岸线，其分形维数大约为1.1。事实上，分形概念的提出者，本华·曼德博（Benoit Mandelbrot）于1967年在《科学》杂志上发表了一篇著名的论文，题目为“英国的海岸线有多长？统计自相似性和分形维数”。简而言之，那些在某种程度上不规则，并表现出自相似性的形体就是分形，它们的维数介于它们本身的维数和它们试图填充的空间的维数之间。在城市中，通过特定形式的发展来填充二维平面，不论是开辟地块还是设立街道，也不论是以何种密度填充，其分形维数都在1到2之间。因此，这个维数，作为分形图形的维数，也成了城市形态的特征。如今，人们越来越倾向于将城市视为建筑师杰作所产生的分形（Batty，1985），并且这种观点在不同语境中，不同尺度范围里不断被重复阐述（Batty and Longley，1994；Frankhauser，1994；Salingaros，2005；Salat，2011）。

然而，从字面意义上看，有一种形态更适合称为分形，这种形态就是由一个形体或者一系列相互关联的形体所形成的图形，这种图形往往是树状的或者是树突状的。如果我们想要将能源从某个中心源运输到许多距离较远的地点，那么建立一个距离中心源越近，存储能力越大的基础设施就越有效率。我们可以非常轻松地用图形来表示这点，因为如果在这16个点周边设置一圈衔接点，而不是让这16个点中每个点都直接与中心源建立连接，那么我们就能够更有效率地将这些连接线集中起来从而最小化中心源与各点之间的距离。在图8.3a中，假设每条连接线的长度为单位1，则连接这些地点（“填充空间”）所需要的连接线的总长度为16个单位，相比之下，如果将这些路线如图8.3b所示集中为两条，然后是四条、八条，则所需的运输路线总长大约为图8.3a中路线总长的二分之一到四分之三，具体为多少取决于具体布局。越靠近中心源的运输路线，运载量越大，因而花费的建造成本也越大。然而，这也说明了很重要的一点：为了节约资源（几乎每个案例都会有这样的考虑），我们必须有效地填充空间。图8.3中的树状结构为分形，图8.3b直接反映了自相似性，也反映了一个在空间上铺展开来的等级结构的建造模式。这与我们第3章中谈及的很多网络是相关的，尤其是交通网络的异速生长，以及我们上一章中探讨的分形网络。

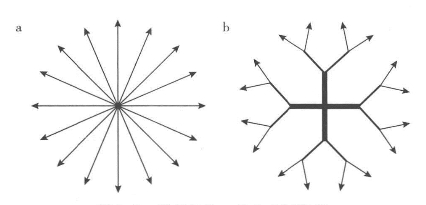
图8.3　等级结构：从中心源输送

注：a.每条运输路线都是独立的；b.将运输路线重新安排形成一个更为有效的结构。

不管是在自然界还是在人类设计建造的体系中，都有许多这种等级结构的例子。如图8.4a中肺系统原理图所示，血液、氧气、电波信号等通过动脉、血管、肺和神经等树状网络被传送到身体的各个部位。如图8.4b所示，植物向上从空气中获取氧气，向下从土壤中获取其他养分。图8.4c更贴近我们的关注点，也反映了我们上文提及的路径系统。图8.4c显示的是一个英格兰小镇伍尔弗汉普顿的街道系统（2001年人口大约为300 000人）。显然，传统的街道系统正在变得越来越有序，其中市镇中心的环形公路是自上而下规划好的，也证明了我们上文提及的观点，城市形态往往是由不同尺度范围内的决策意见所塑造的。图8.4d为建筑公司棕榈岛集团在迪拜海岸外建造的一系列棕榈岛之一。这个例子很好地说明了在填海造陆时节约资源的必要性，在这个案例中，交通和能源输送是主要的障碍。

这些案例补充说明了第3章中介绍的网络，但是在这里我们强调的是这些网络的演化和生长动态，这些网络大部分都是自下而上建立的，只有一小部分是自上而下规划建立的。在城市发展的过程中，不论在哪个时间点上，我们都很难得知城市将来可能形成的社会行为，价值观念，技术水平和社会规范。所以，城市发展的方式往往反映了其发展时主导的理念，彼时的效率和公平状态。为了说明我们如何根据这一过程建模，我们可以抽象概括出两种主要驱动力，一种是任一个人、开发商或者消费者对空间的需求，与之相对的是想要离“城市”尽可能近以实现规模经济的需求。这是一个简单的模型，在第1章中我们也提到了。这个模型反映了我们至今所提及的所有概念，现在我们将进一步把这个模型发展成一个模拟模型。

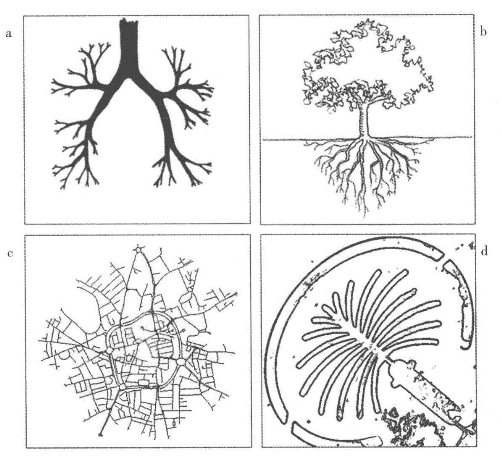
图8.4　空间填充等级体系

注：a.人类肺系统原理图；b.树内部运输系统原理图，上方为空气，下方为土壤；c.英格兰小镇伍尔弗汉普顿的街道网络；d.棘手媒介上的空间填充：棕榈岛集团在迪拜建造的棕榈岛。