重积分的定义及性质
(1)定义
二重积分的定义
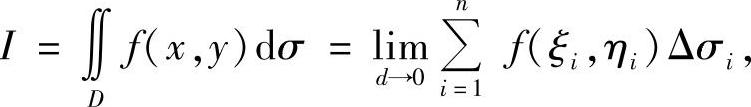
其中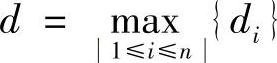 ,di是Δσi的直径,(ξi,ηi)∈Δσi称为介点(i=1,2,…,n).
,di是Δσi的直径,(ξi,ηi)∈Δσi称为介点(i=1,2,…,n).
几何意义:当z=f(x,y)≥0,(x,y)∈D时,二重积分I表示以z=f(x,y)为曲顶,以D为底面的曲顶柱体的体积.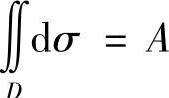 ,A为D的面积.
,A为D的面积.
三重积分的定义
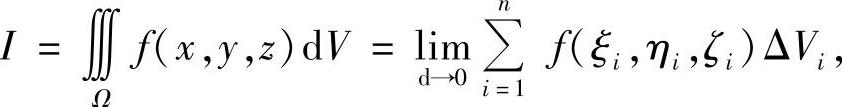
其中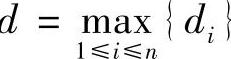 ,di是ΔVi的直径,(ξi,ηi,ζi)∈ΔVi称为介点(i=1,2,…,n).
,di是ΔVi的直径,(ξi,ηi,ζi)∈ΔVi称为介点(i=1,2,…,n).
物理意义:当u=f(x,y,z)≥0,(x,y,z)∈Ω时,三重积分I表示以u=f(x,y,z)为体密度的空间物体Ω的质量.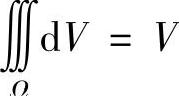 , V为Ω的体积.
, V为Ω的体积.
(2)重积分的性质
重积分的许多性质和定积分是一样,如线性性、区域的可加性、不等式性与绝对可积性、中值定理等.对此我们不再一一列举,下面给出重积分的对称定理.
二重积分的对称定理 设D是平面上的有界闭区域,函数f(x,y)在D上可积,则
1)若D=D1+D2,D1与D2关于y轴对称,那么
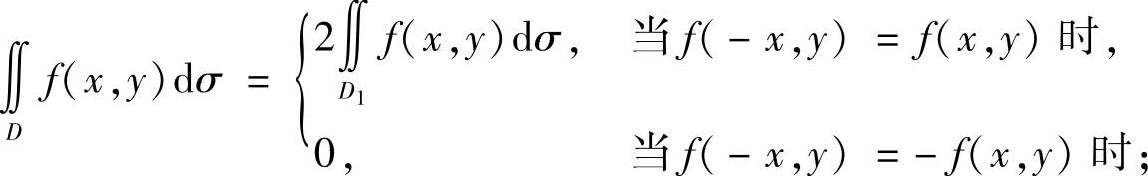
2)若D=D1+D2,D1与D2关于x轴对称,那么
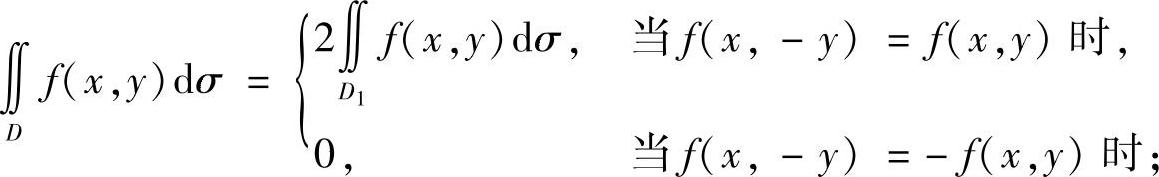
3)若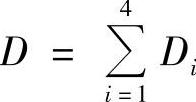 是关于x轴、y轴均对称的区域,那么
是关于x轴、y轴均对称的区域,那么
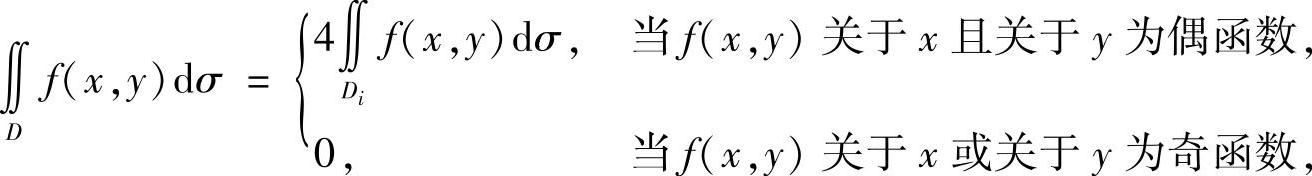
其中Di是区域D位于第i(i=1,2,3,4)象限的区域;
4)若D=D1+D2,D1与D2关于原点对称,那么
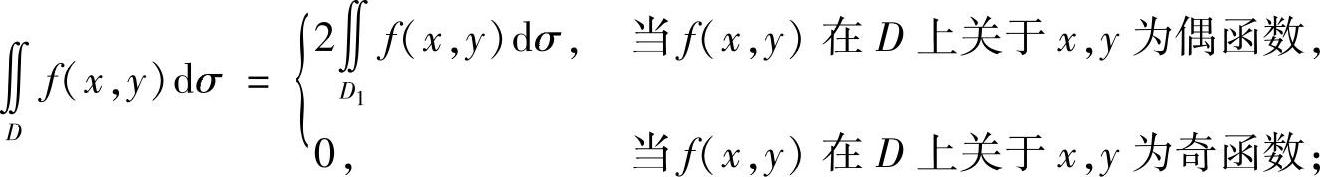
5)若D关于直线y=x对称,则
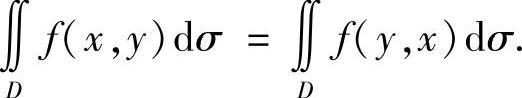
三重积分的对称定理 设Ω是三维空间的有界闭区域,f(x,y,z)在Ω上可积,则
1)若Ω=Ω1+Ω2,Ω1与Ω2关于xOy平面对称,那么
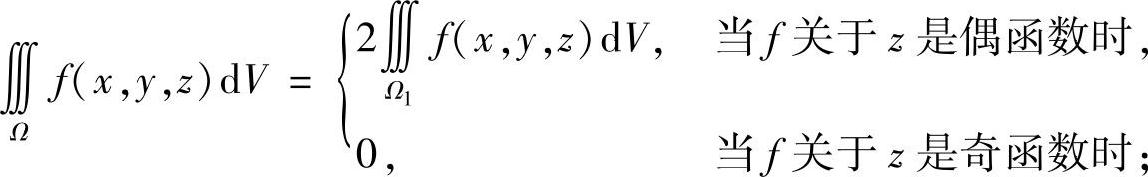
2)若Ω=Ω1+Ω2,Ω1与Ω2关于z轴对称,那么
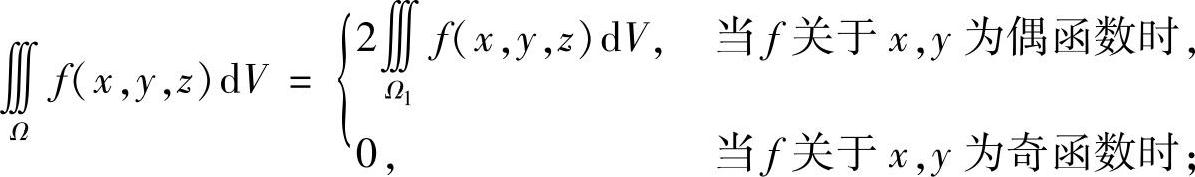
3)若Ω=Ω1+Ω2,Ω1与Ω2关于原点对称,那么
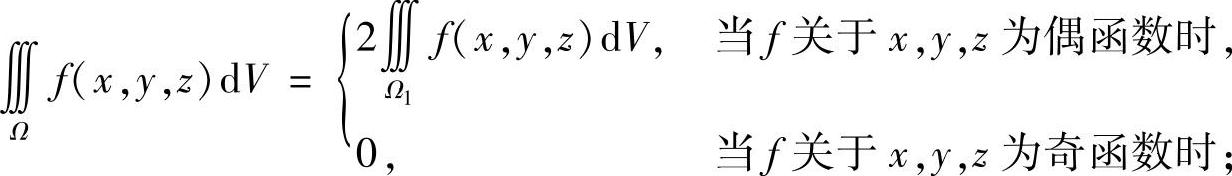
4)若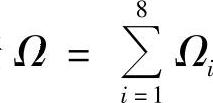 是关于三个坐标平面均对称的区域,那么
是关于三个坐标平面均对称的区域,那么

其中Ωi表示Ω在第i(i=1,2,…,8)卦限的那部分区域.
需要指出的是,仅当积分区域的对称性和被积函数的奇偶性同时满足时,才能使用重积分的对称定理.
(3)二重积分的计算
计算二重积分的基本方法是:化成累次积分.而化累次积分的方法是根据积分区域D的形状来确定的.
若D=[a,b]×[c,d]为矩形区域,则有
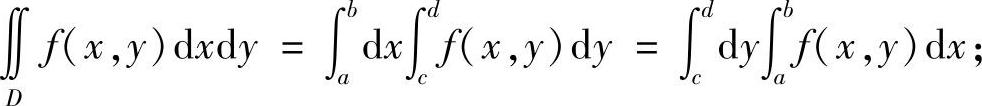
若D={(x,y)a≤x≤b,φ1(x)≤y≤φ2(x)}为X型区域,则有
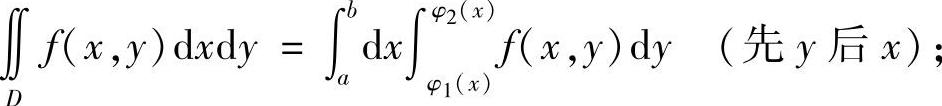
若D={(x,y)ψ1(y)≤x≤ψ2(y),c≤y≤d}为Y型区域,则有
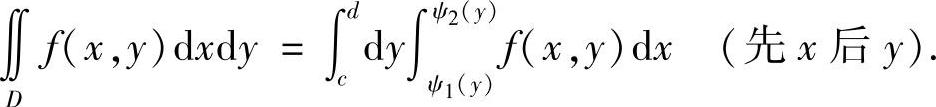
两点说明:(a)积分区域D从整体来看,它可能既不是X型也不是Y型区域,但总可分为若干个X型或Y型区域.利用积分区域的可加性先在每个小的X型或Y型区域上计算,然后相加即可.
(b)不同顺序的累次积分,计算的复杂程度差别非常大(可能某一顺序的累次积分无法积出!)因此选择合适的积分顺序是重要的.
另外,在计算重积分时,要注意使用对称定理和几何意义(主要指重心或形心)来提高运算的速度.
二重积分的变量替换定理 设变换
T:x=x(u,v),y=y(u,v),(u,v)∈D′.
满足:1)T建立了D与D′之间的一一对应;
2)x,y在D′上具有一阶连续偏导数,其逆变换u=u(x,y),v=v(x,y)在D上具有一阶连续偏导数;
3)T的Jacobi行列式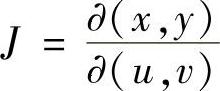 在D′上恒不为零,则
在D′上恒不为零,则
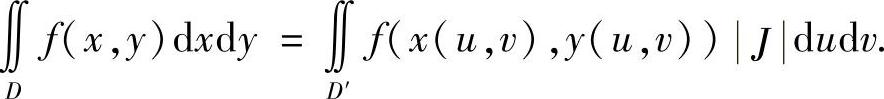
满足上述要求的变换T称为正则变换.
在二重积分的计算中,最常用的变换是极坐标变换或广义极坐标变换.
例7.25 作极坐标变换,将二重积分
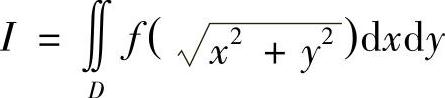
化为定积分,其中D={(x,y)0≤y≤x≤1}.
解 如图7-1所示.令x=rcosθ,y=rsinθ,则
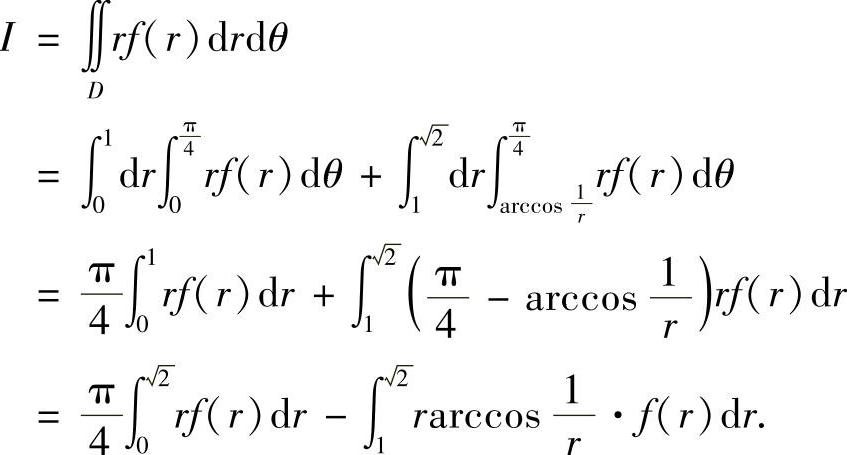
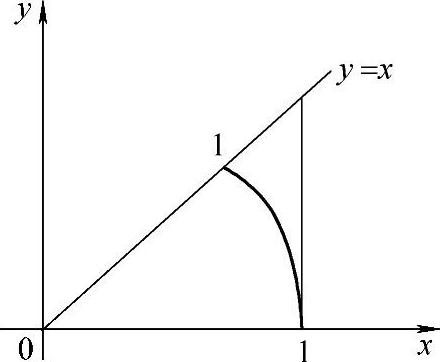
图7-1 例7.27图
例7.26 将下面的二重积分化为定积分:
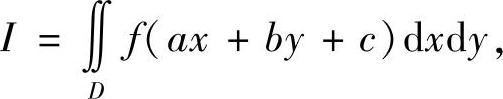
其中D={(x,y)x2+y2≤1},a2+b2≠0.
解 作正交变换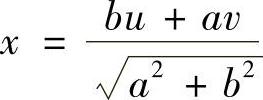 ,
,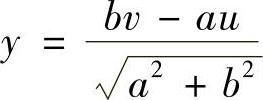 ,则
,则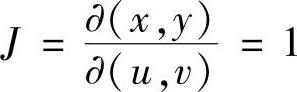 ,xy平面上的区域D变成了uv平面上的区域D′:u2+v2≤1.于是有,
,xy平面上的区域D变成了uv平面上的区域D′:u2+v2≤1.于是有,
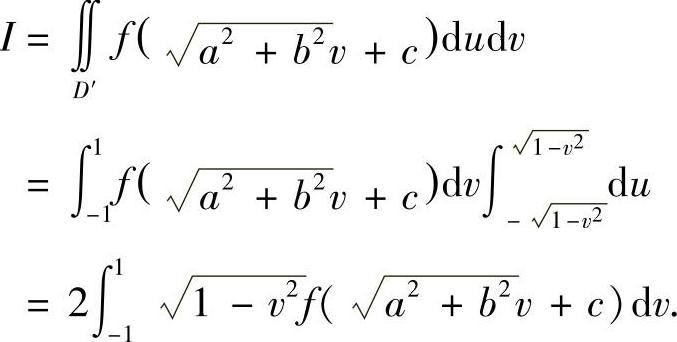
例7.27 设区域D是由y=x3,y=1及x=-1所围成,f(u)是连续函数.计算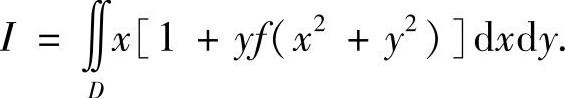
解 如图7-2所示.由于被积函数中出现了抽象函数,所以直接计算是行不通的.因此必须考虑用对称定理,为此需要对区域进行适当的分割.
用y=-x3将区域D分为D1和D2两部分,其中D1关于y轴对称,D2关于x轴对称.故
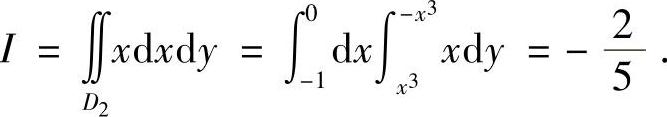
类题1 求二重积分
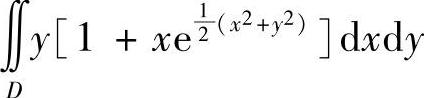
的值,其中D是由直线y=x,y=-1和x=1所围成的区域(数学Ⅲ,Ⅳ).
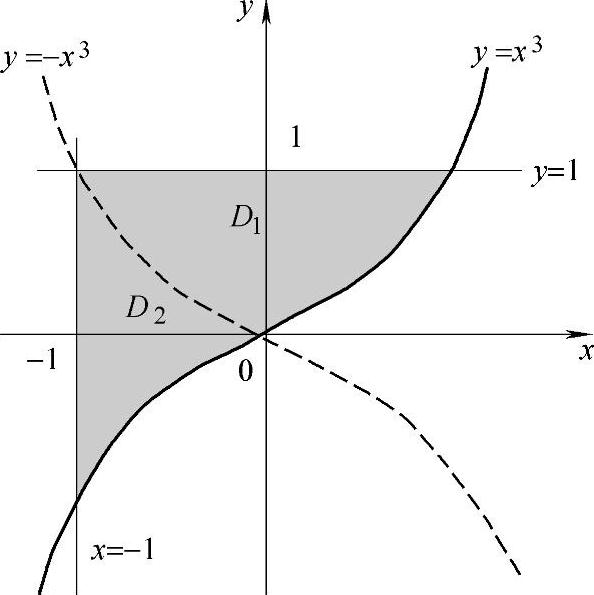
图7-2 例7.29图
类题2 选择题:设D是xy平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形区域,D1是D在第一象限的部分,则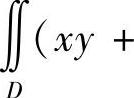
例7.28 计算积分
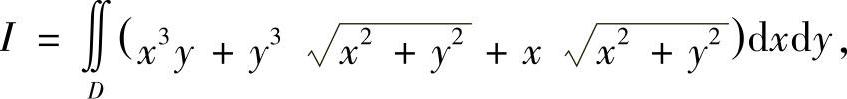
其中D:x2+y2≤ax.
解 因为积分区域D关于x轴对称,而x3y,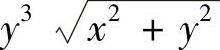 是关于y的奇函数,故
是关于y的奇函数,故
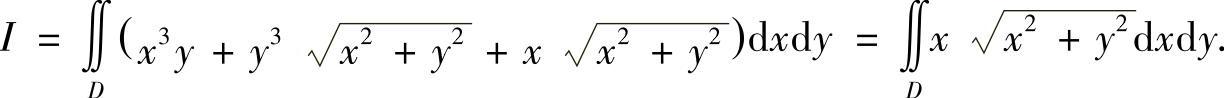
作极坐标变换:x=rcosθ,y=rsinθ,则
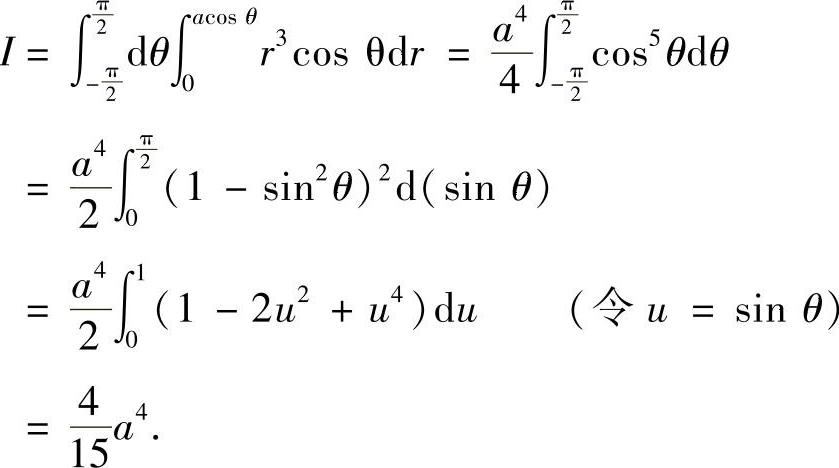
例7.29 计算由曲线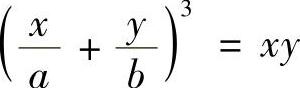 所围的区域D的面积(a>0,b>0).
所围的区域D的面积(a>0,b>0).
解 任一条直线y=kx(k>0)与曲线有两个交点(0,0)与
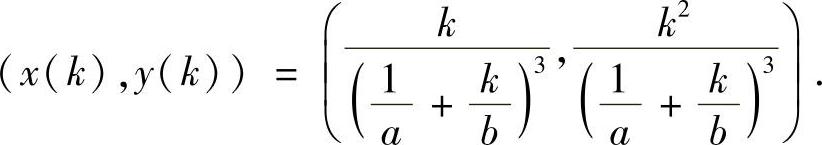
由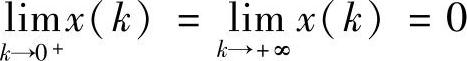 ,
,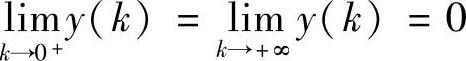 知,曲线所围的区域位于第一象限内.作变换:
知,曲线所围的区域位于第一象限内.作变换:
x=arcos2θ,y=brsin2θ,
则
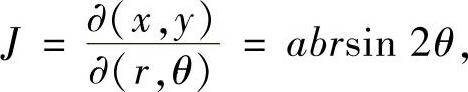
区域D变成区域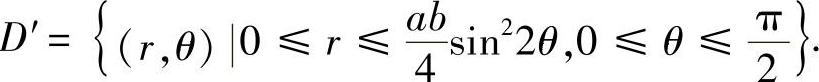 于是,区域D的面积
于是,区域D的面积
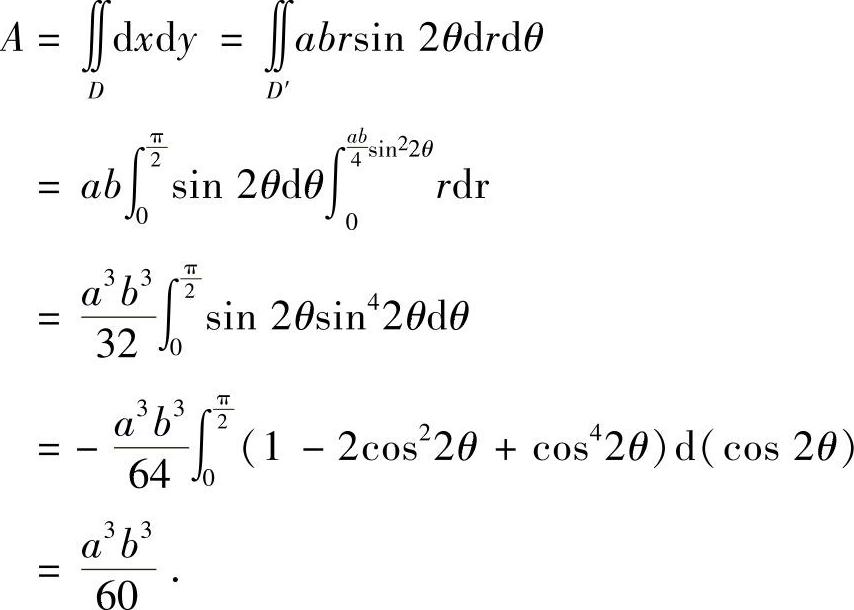
注7.5 这个题目的计算,我们作了广义极坐标变换.一般地,对形如(ax-c)p+(by-d)p函数式子可通过变换:
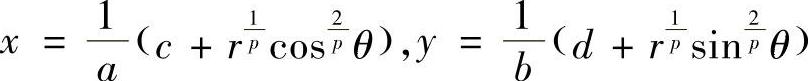
将它变为r.
类题1 求由曲线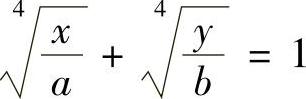 与直线x=0,y=0所围的区域面积.
与直线x=0,y=0所围的区域面积.
提示 作变换:x=ar4cos8θ,y=br4sin8θ.
类题2 求积分
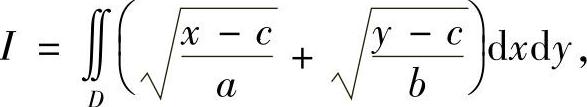
其中D是由曲线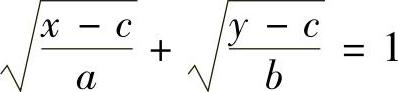 和直线x=c,y=c所围成,而a,b,c>0.
和直线x=c,y=c所围成,而a,b,c>0.
提示 作变换:x=c+ar2cos4θ,y=c+br2sin4θ.
例7.30 计算
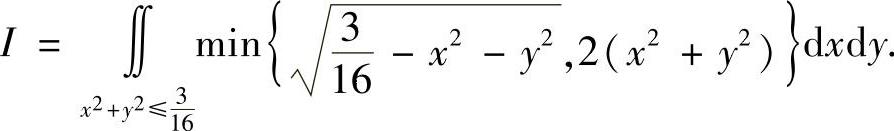
解 因为
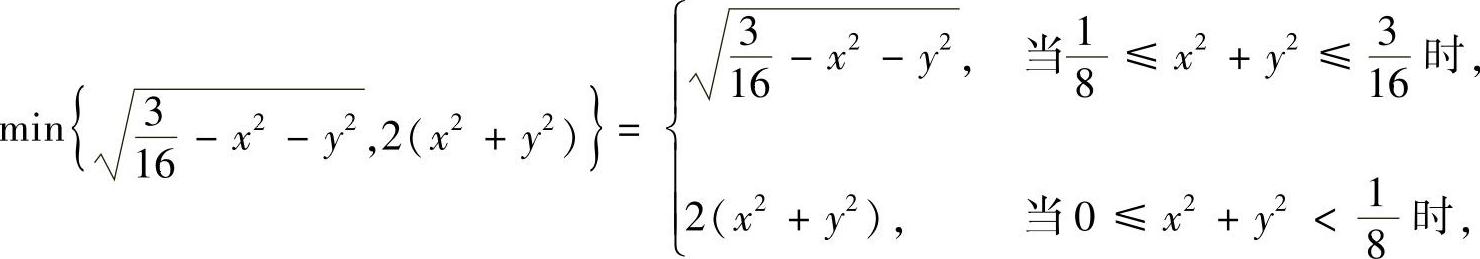
所以
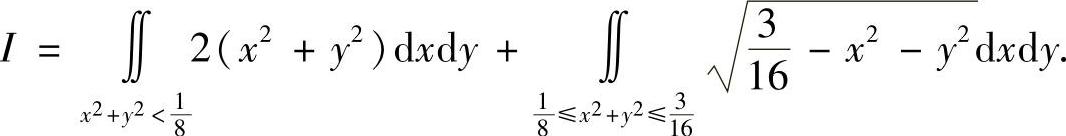
作极坐标变换:x=rcosθ,y=rsinθ,则有
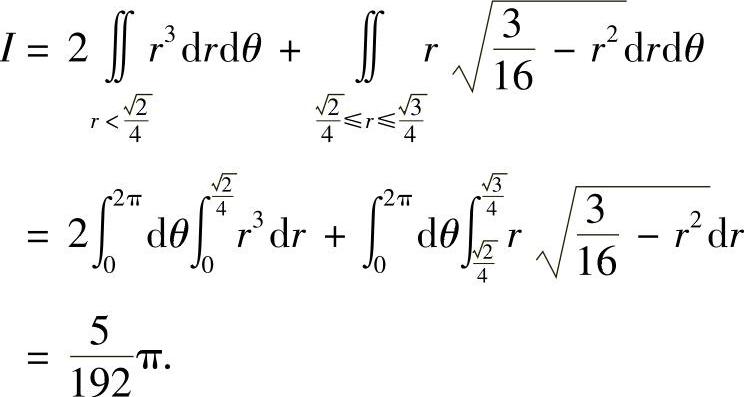
例7.31 1)计算积分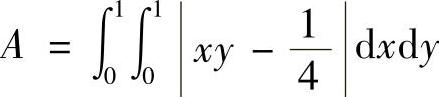 ;
;
2)设z=f(x,y)在闭正方形D:0≤x≤1,0≤y≤1上连续,且满足下列条件: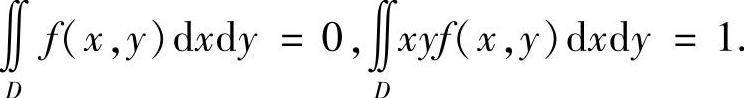 证明存在(ξ,η)∈D,使得
证明存在(ξ,η)∈D,使得
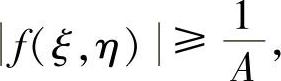
这里A是1)中的积分值(北大).
1)解 如图7-3所示.
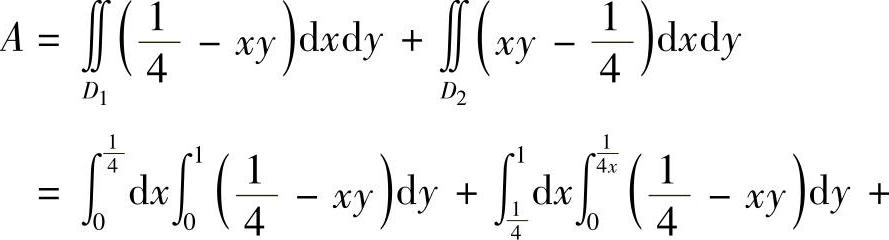
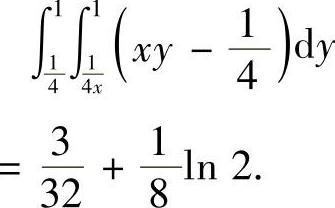
2)证明 由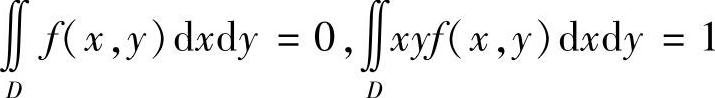 知,
知,
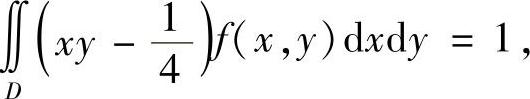
所以
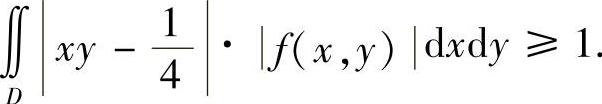
由积分中值定理知,存在(ξ,η)∈D,使
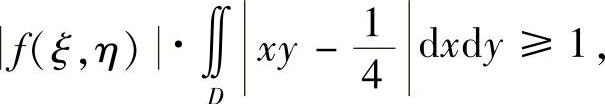
故
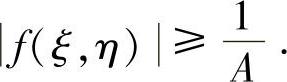
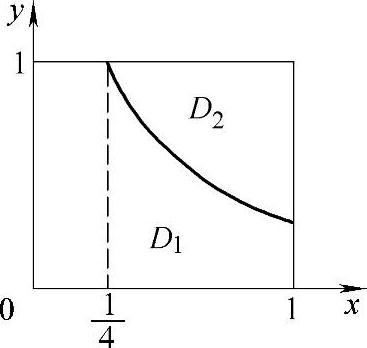
图7-3 例7.33图
例7.32 计算积分
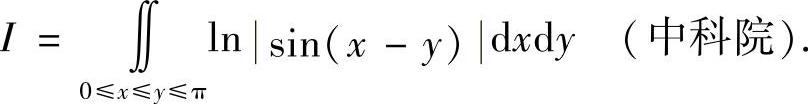
解 由对称性,有
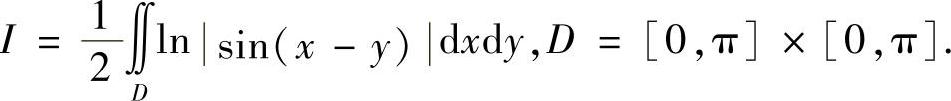
而

例7.33 计算二重积分
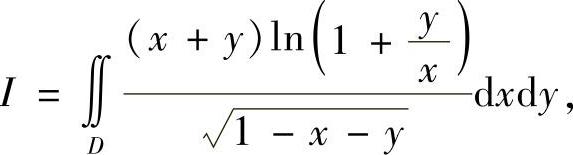
其中D表示由直线x+y=1及两坐标轴所围成的三角形区域(复旦).
解 作变换:u=x+y,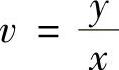 ,则
,则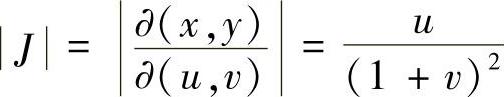 ,而积分区域D变成了uv平面上的区域Ω={(u,v)0≤u≤1,0≤v<+∞}.于是,有
,而积分区域D变成了uv平面上的区域Ω={(u,v)0≤u≤1,0≤v<+∞}.于是,有
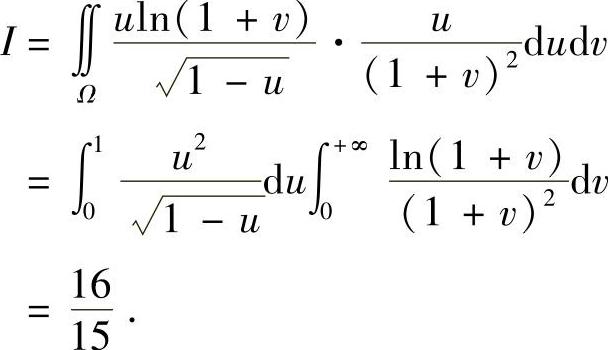
类题 求曲线C:∣lnx∣+∣lny∣=1所围的平面图形面积A.
提示 曲线C所围的平面区域D位于第一象限.
当x≥1,y≥1时,C的方程为:lnx+lny=1,即xy=e;
当x≥1,0<y<1时,C的方程为:lnx-lny=1,即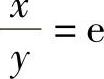 ;
;
当0<x<1,y≥1时,C的方程为:-lnx+lny=1,即 ;
;
当0<x<1,0<y<1时,C的方程为:-lnx-lny=1,即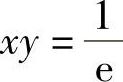 .
.
这四条曲线构成了区域D的边界,于是有
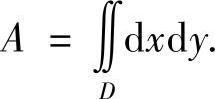
作变换:u=xy,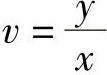 ,则变换的Jacobi式为
,则变换的Jacobi式为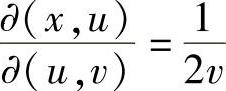 ,区域D变成了uv平面的区域
,区域D变成了uv平面的区域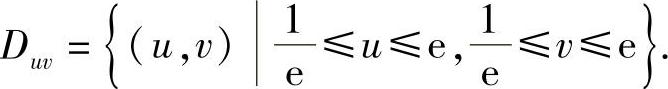 所以
所以
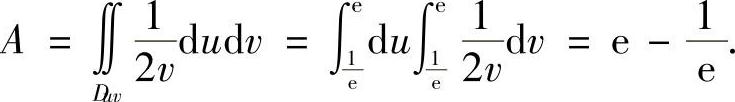
例7.34 给定积分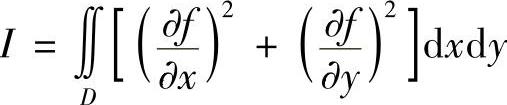 ,作正则变换x=x(u,v),y=y(u,v),区域D变为Ω,如果变换满足
,作正则变换x=x(u,v),y=y(u,v),区域D变为Ω,如果变换满足
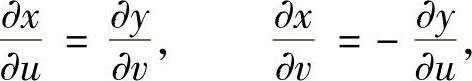
证明:
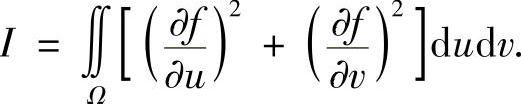
(北师大).
证明 利用复合函数的微分法,有
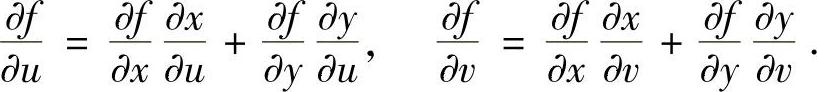
通过计算易知
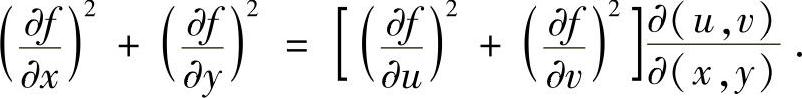
注意到
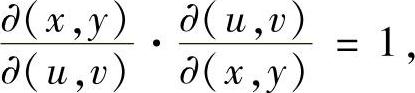
可得
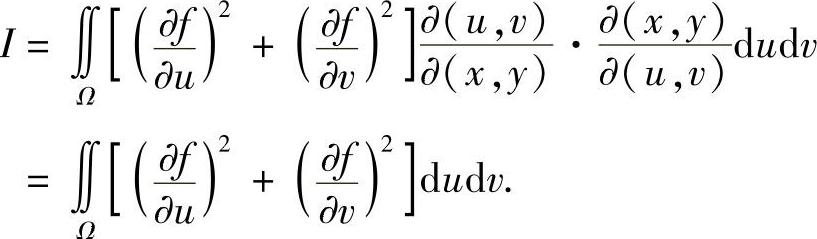
例7.35 设f是{(x,y)x2+y2≤1}上的二次连续可微函数,且满足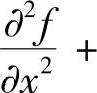
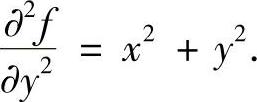 计算积分
计算积分
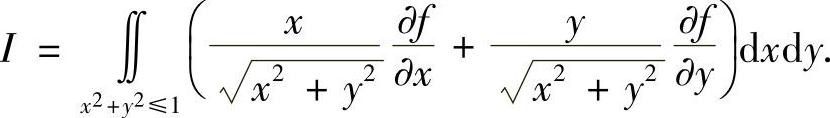
(复旦):
解 作极坐标变换:x=rcosθ,y=rsinθ,则
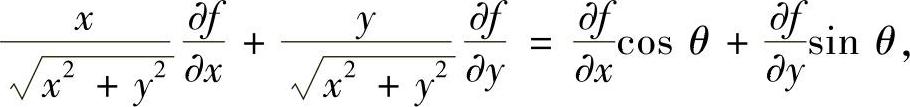
所以
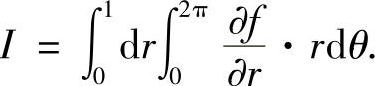
利用格林公式,有
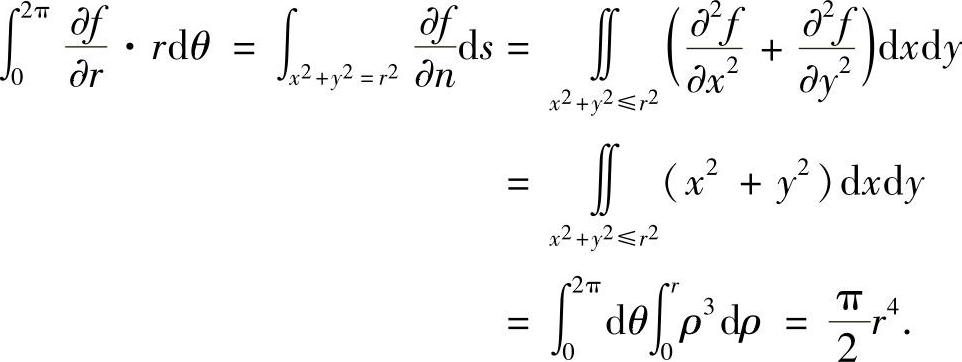
于是
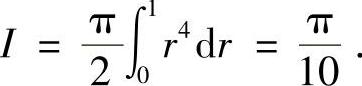
类题1 设f(x,y)在x2+y2≤1二次连续可微,且满足
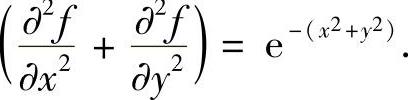
试计算积分
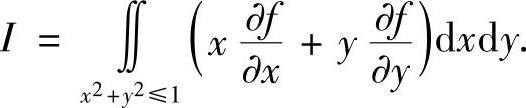
类题2 设函数z=f(x,y)满足方程F(x+az,y+bz)=0,其中F为可微函数,a,b为常数,求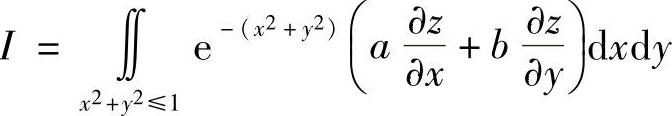 (华南理工).
(华南理工).
提示 在方程F(x+az,y+bz)=0两边分别关于x,y求偏导,可得
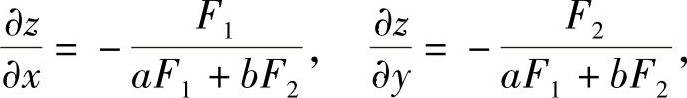
进而有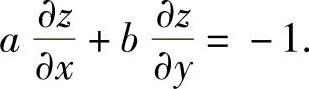 于是,
于是,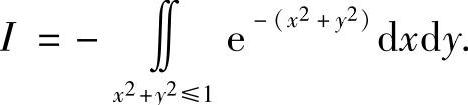
例7.36 计算积分
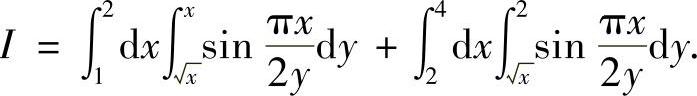
(数学Ⅱ).
解 积分区域D是由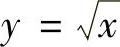 ,y=x及y=2所围成(如图7-4所示).交换累次积分的顺序,有
,y=x及y=2所围成(如图7-4所示).交换累次积分的顺序,有
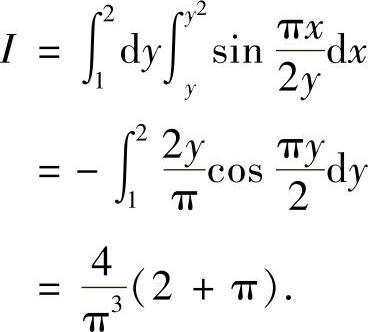
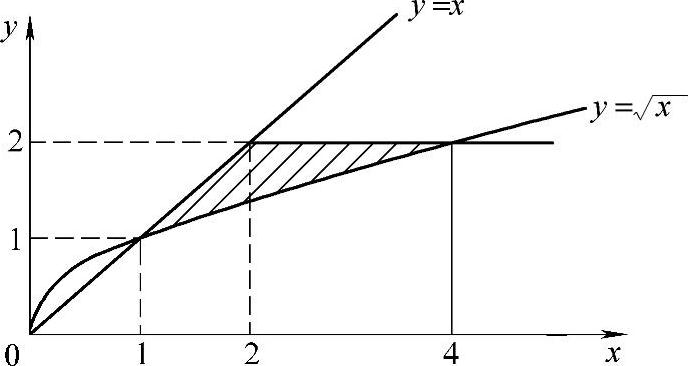
图7-4 例7.38图
注7.6 计算累次积分的一般步骤:根据积分的上、下限得到表示积分区域D的不等式组,并由此画出积分区域的草图.然后根据积分区域的类型选择合适的积分顺序.
(4)三重积分的计算.
计算三重积分的基本方法是:化为累次积分(先一后二或先二后一).在化累次积分时要注意选择适当的坐标系(直角坐标、柱坐标、球坐标)和合适的积分顺序.
在计算三重积分时类似于二重积分的变量替换定理也成立,在此不再赘述.常用的变量变换有
柱坐标变换
x=rcosθ,y=rsinθ,z=z,∣J∣=r,
0≤r<+∞, 0≤θ<2π,-∞<z<+∞.
由此可见,柱坐标变换就是z不变,而将x,y用极坐标变换.因此,将三重积分先对z积分化成二重积分(先一后二)后,再用极坐标变换其结果是一样的.
当然,相应于柱坐标变换也有广义柱坐标变换.
球坐标变换
x=rsinφcosθ, y=rsinφsinθ, x=rcosφ, ∣J∣=r2sinφ,
0≤r<+∞, 0≤θ<2π, 0≤φ≤π,(https://www.xing528.com)
其中r是球半径,θ是转动角,φ是仰角(即与z轴正向的夹角).
另外,相应于球坐标变换也有广义球坐标变换.
(5)重积分的应用.
几何上的应用
1)求平面区域D的面积,即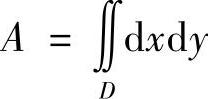 ;
;
2)求空间区域Ω的体积,即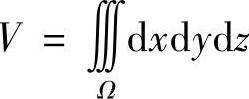 ;
;
3)求曲面的面积.
设二元函数z=f(x,y)及其一阶偏导数都连续,它所对应的曲面S与平行于z轴的直线只交于一点,Dxy为该曲面在xOy平面上的投影,则曲面S的面积为
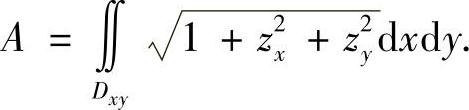
在物理上的应用
1)求质量
薄片的质量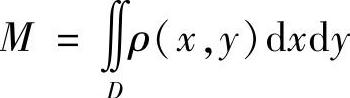 ,其中ρ(x,y)≥0是薄片的面密度.
,其中ρ(x,y)≥0是薄片的面密度.
空间立体的质量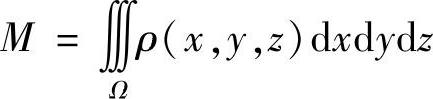 ,其中ρ(x,y,z)≥0是空间立体的体密度;
,其中ρ(x,y,z)≥0是空间立体的体密度;
2)求重心.
薄片的重心
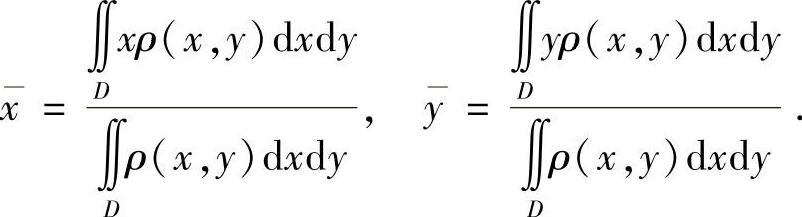
空间立体的重心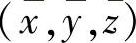
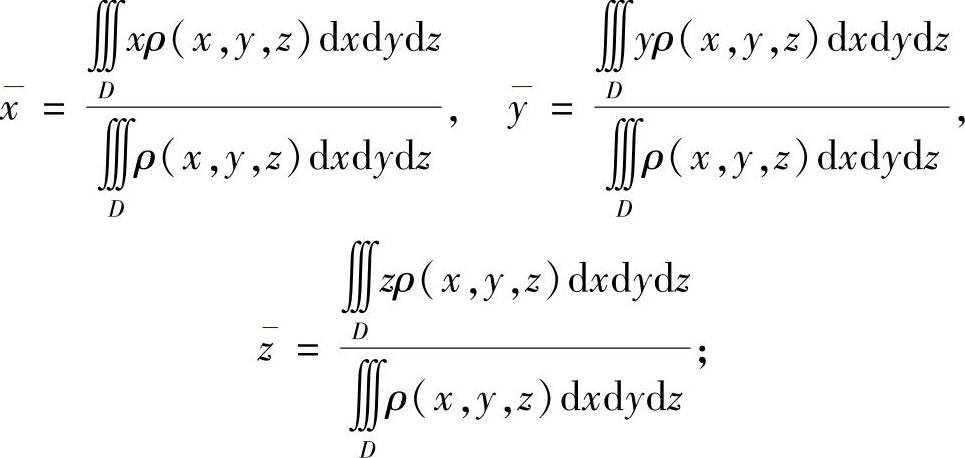
3)求转动惯量
薄片关于x轴,y轴及原点的转动惯量分别为:
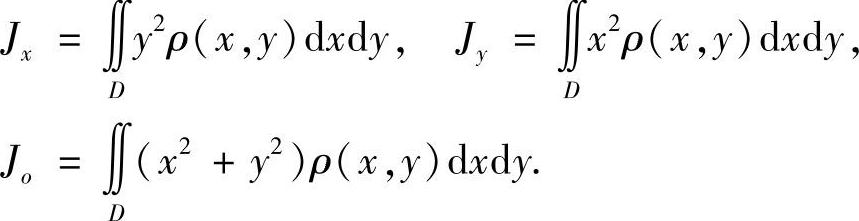
空间立体关于x,y,z轴及原点的转动惯量分别为:
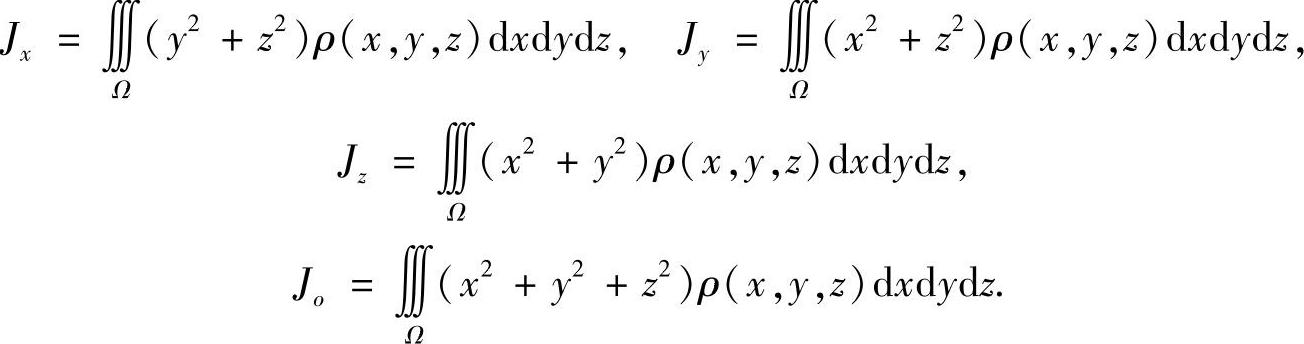
例7.37 计算三重积分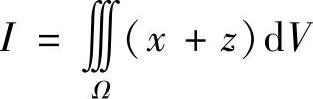 ,其中Ω是由曲面
,其中Ω是由曲面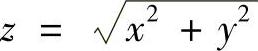 与
与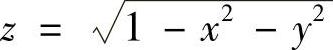 所围的区域(数学Ⅰ).
所围的区域(数学Ⅰ).
解 由于积分区域Ω关于yOz平面对称,所以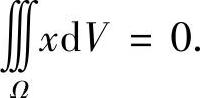 对积分
对积分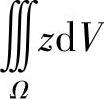 采用“先二后一”的方法,则有
采用“先二后一”的方法,则有
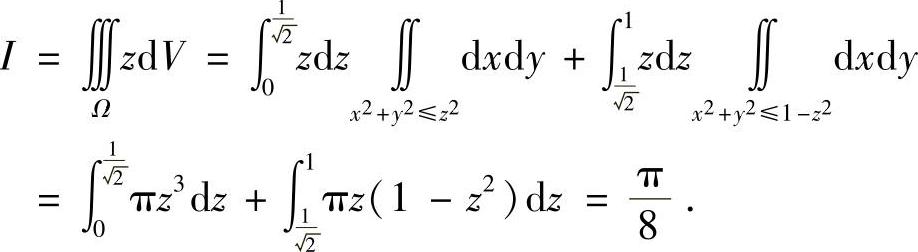
本例亦可用球坐标变换和柱坐标变换来求解.
类题1 计算三重积分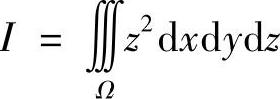 ,其中Ω为球体x2+y2+z2≤R2和x2+y2+z2≤2Rz(R>0)的公共部分.
,其中Ω为球体x2+y2+z2≤R2和x2+y2+z2≤2Rz(R>0)的公共部分.
提示 用“先二后一”法.
当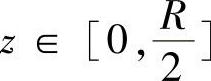 时,用z=z的平面去截Ω,截口是圆域D1(z):x2+y2≤2Rz-z2;
时,用z=z的平面去截Ω,截口是圆域D1(z):x2+y2≤2Rz-z2;
当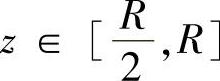 时,用z=z的平面去截Ω,截口也是圆域D2(z):x2+y2≤R2-z2.于是,有
时,用z=z的平面去截Ω,截口也是圆域D2(z):x2+y2≤R2-z2.于是,有
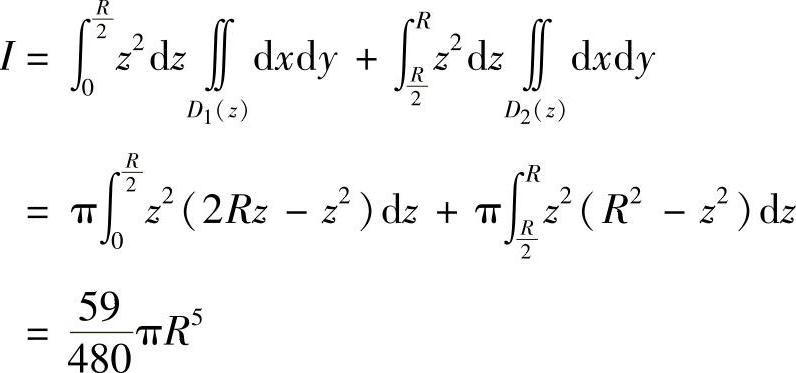
类题2 计算三重积分: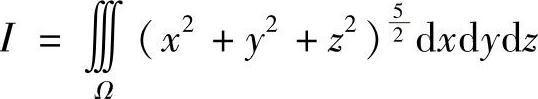 ,其中Ω:x2+y2+(z-1)2≤1.
,其中Ω:x2+y2+(z-1)2≤1.
提示 用“先二后一”法.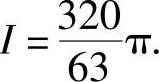
例7.38 设有一高度为h(t)(t为时间)的雪堆在融化过程中,其侧面满足方程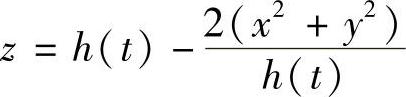 (设长度单位为cm,时间单位为h).已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130cm的雪堆全部融化需多长时间?(数学Ⅱ).
(设长度单位为cm,时间单位为h).已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130cm的雪堆全部融化需多长时间?(数学Ⅱ).
解 设V(t)为雪堆的体积,S(t)为雪堆的侧面积,则
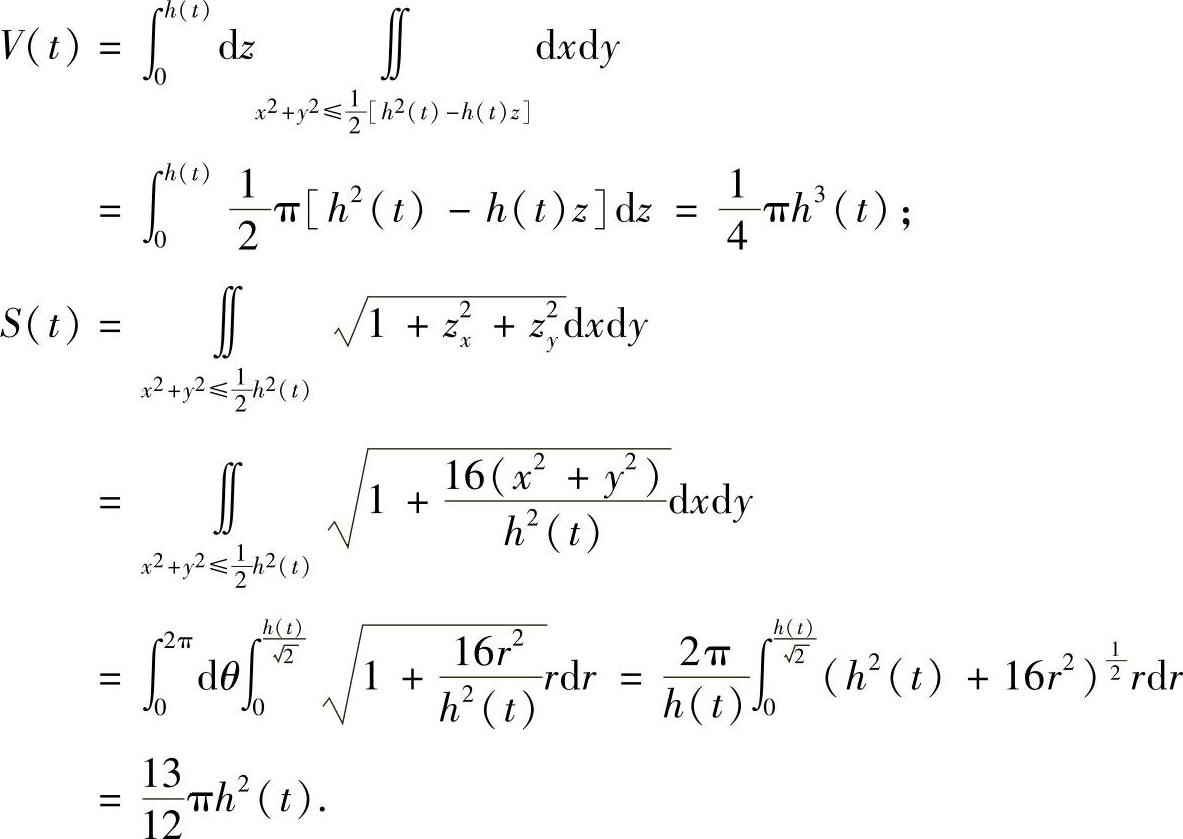
由题意知,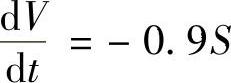 ,即
,即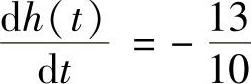 ,解之可得
,解之可得
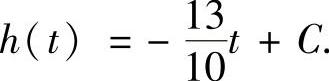
由初始条件h(0)=130,可得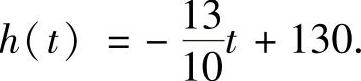 令h(t)→0可得t=100(h).故雪堆全部融化所需的时间为100h.
令h(t)→0可得t=100(h).故雪堆全部融化所需的时间为100h.
例7.39 设有一半径为R的球体,P0是此球的表面上的一定点,球体上任一点的密度与该点到P0的距离的平方成正比(比例常数k>0),求球体的重心位置(数学Ⅰ).
解法1 记所考虑的球体为Ω,以Ω的球心为坐标原点O,射线OP0为x轴的正向建立坐标系,则P0点的坐标为(R,0,0),球面方程为
x2+y2+z2=R2.
密度函数为
ρ(x,y,z)=k[(x-R)2+y2+z2].
设重心坐标为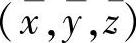 ,由对称性可知,y=0,z=0,
,由对称性可知,y=0,z=0,
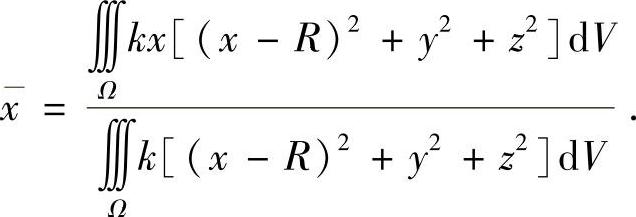
而
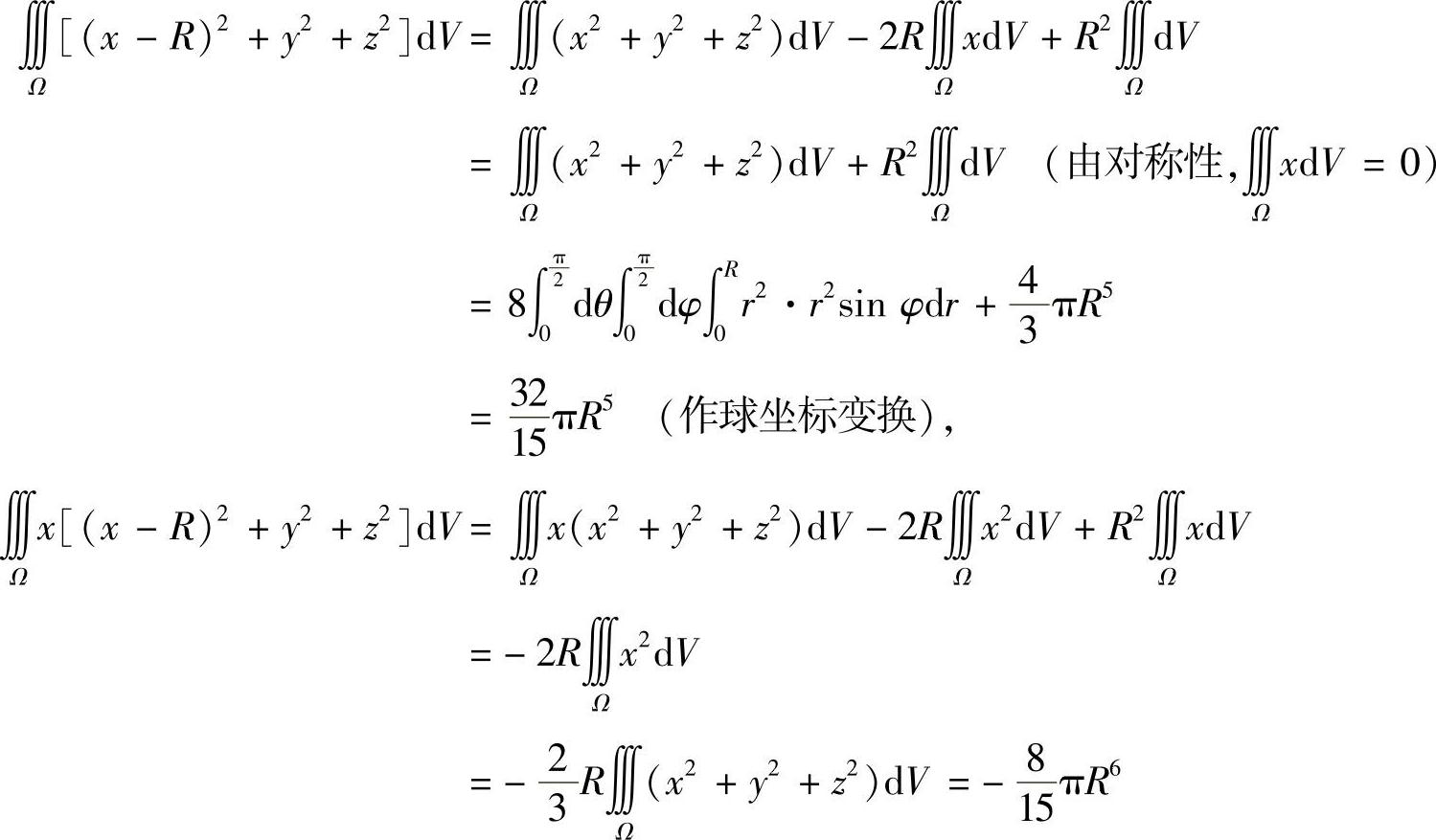
故
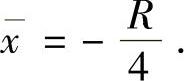
因此球体Ω的重心位置为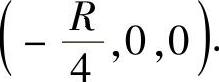
解法2 选取P0为坐标系的原点,球心坐标为(0,0,R),则球面方程为
x2+y2+(z-R)2=R2.
而此时密度函数为
ρ(x,y,z)=k(x2+y2+z2).
设重心坐标为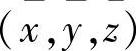 ,由对称性知,x=0,y=0,
,由对称性知,x=0,y=0,
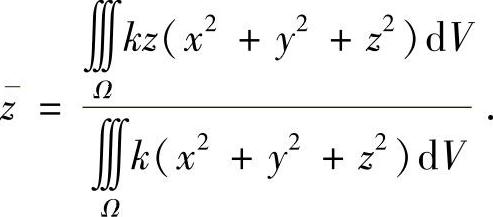
而
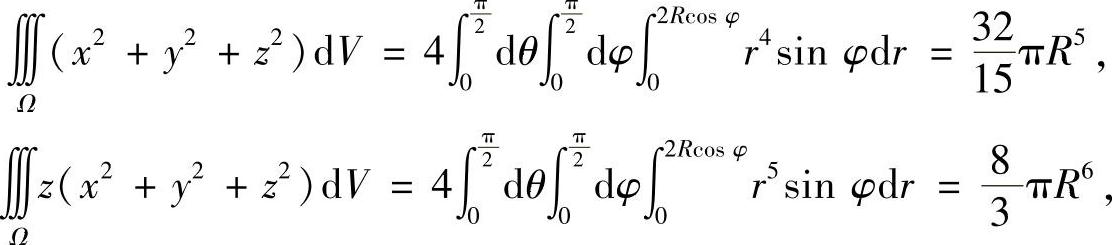
故
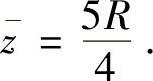
因此球体Ω的重心坐标为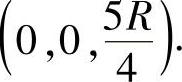
注7.7 求重心问题,虽然有固定的方法,但是坐标系的选择是至关重要的,合适的坐标系可使问题大大简化.在解法1中,我们多次使用了对称性的结论.
类题 计算三重积分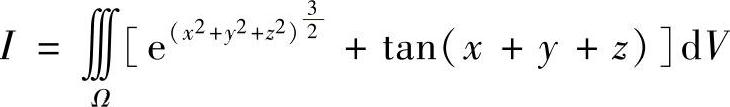 ,其中Ω={(x,y,z)x2+y2+z2≤1}.
,其中Ω={(x,y,z)x2+y2+z2≤1}.
提示 断言: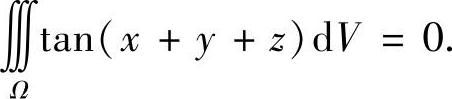
易见Ω关于平面Π:x+y+z=0对称,只要能证明tan(x+y+z)在关于Π的对称点处的值相反即可.
设(x0,y0,z0)∈Ω,其关于Π的对称点设为(x1,y1,z1),则点(x1,y1,z1)必在直线L: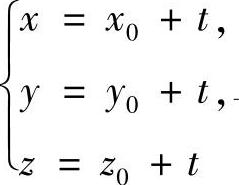 上,将其代入Π的方程可得:
上,将其代入Π的方程可得: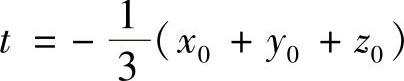 ,所以L与Π的交点为
,所以L与Π的交点为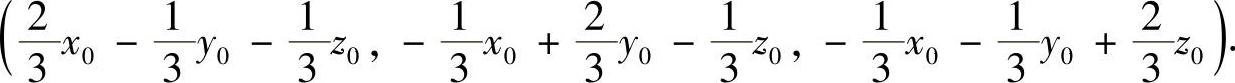
由
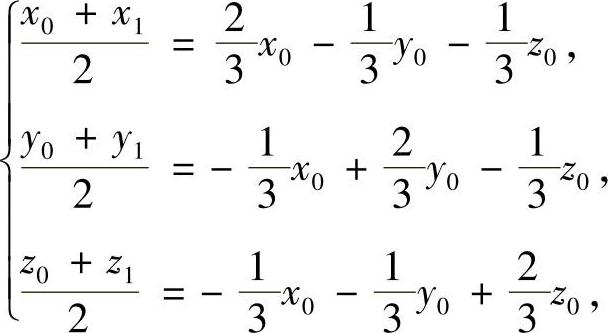
可得
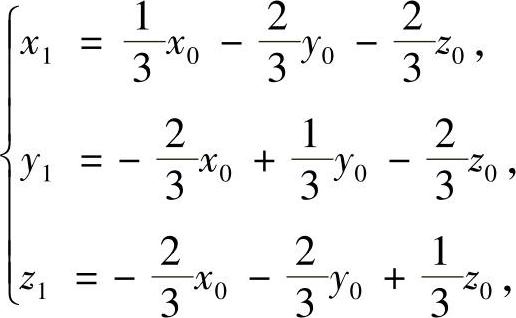
所以tan(x1+y1+z1)=tan(-x0-y0-z0)=-tan(x0+y0+z0),即tan(x+y+z)在关于Π对称的点处的值相反.
于是,有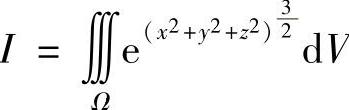 ,用球坐标变换易得:
,用球坐标变换易得: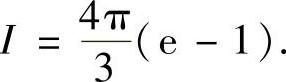
例7.40 计算三重积分
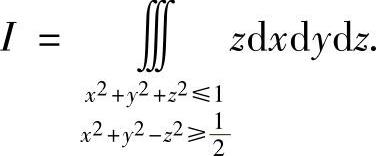
(中科院,1983).
解 用柱坐标变换.不难看出,积分区域Ω变成
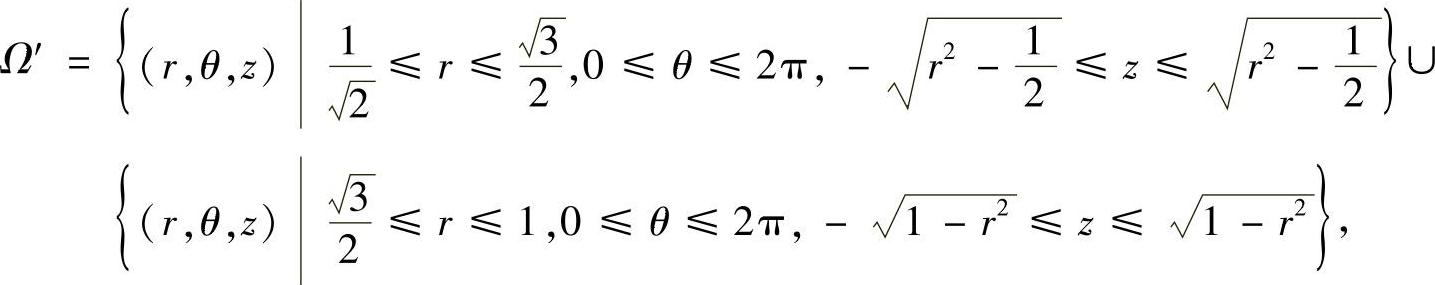
于是有
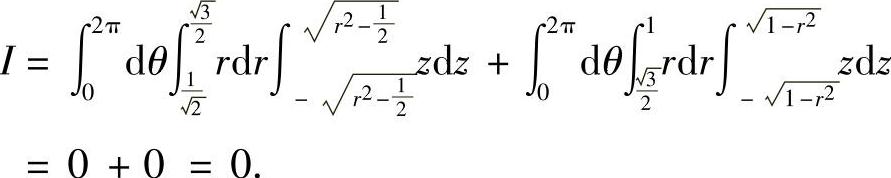
事实上,由于积分区域Ω关于xOy平面对称,而被积函数关于z为奇函数,所以由对称性可知I=0.
例7.41 求由(x2+y2)2+z4=y所围的立体的体积(南开).
解 显然立体关于xOy平面、yOz平面对称.在上半空间y≥0上,用Ω表示位于第一卦限部分的区域,则
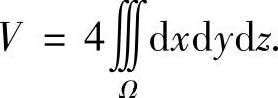
作广义球坐标变换:
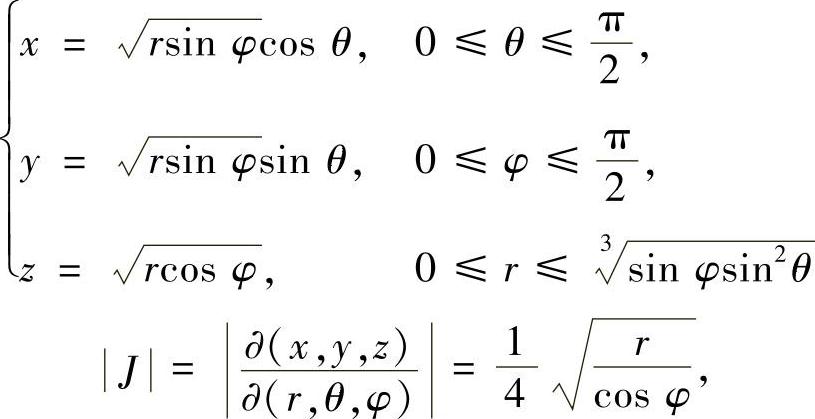
故

例7.42 设a,b,c为不全为零的实数,f(t)是连续函数.
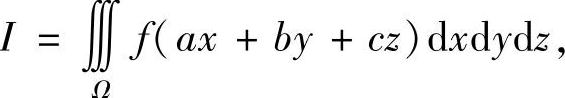
其中Ω:x2+y2+z2≤1.
(1)将I化为单重积分;
(2)当f(t)=cost时,计算I的值(第(2)问,南开).
(3)记第(2)问的结果为I(k),证明:I(k)在(0,+∞)内有无穷多个零点.
解 (1)记 ,把单位向量
,把单位向量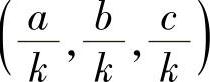 扩充为一个正交矩阵
扩充为一个正交矩阵
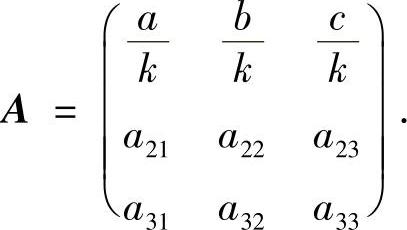
作变换
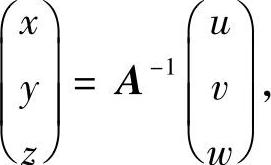
由于A-1仍然是正交阵,故|J=detA-1|=1,且该变换将区域Ω变成区域Ω′:u2+v2+w2≤1.于是
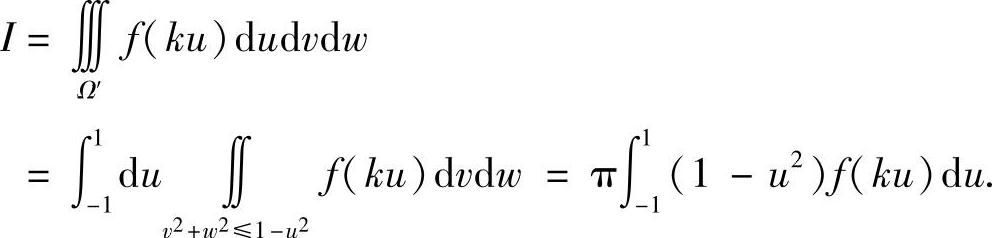
例题7.26是这个问题的二维情形.
(2)当f(t)=cost时,有
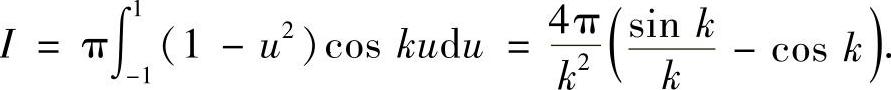
(3)记g(k)=sink-kcosk,只需证明:g(k)在(0,+∞)内有无穷多个零点即可.令g′(k)=ksink=0,可得g(k)的驻点:k=nπ,n∈N.易见
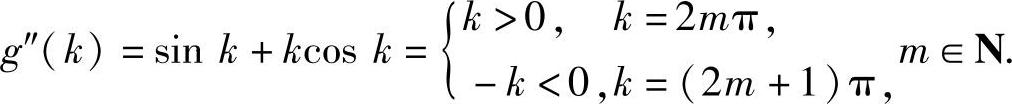
由此可见,g(k)在(0,+∞)内有无穷多个极大值和无穷多个极小值.
而极大值g((2m+1)π)=k>0,极小值g(2mπ)=-k<0.由于g(k)是连续函数,所以它在(0,+∞)内必与x轴有无穷多个交点,即g(k)在(0,+∞)内有无穷多个零点.
例7.43 设A=(aij)3×3是正定矩阵,证明椭球体
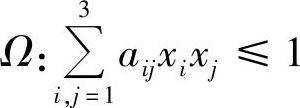
的体积等于 ,即
,即
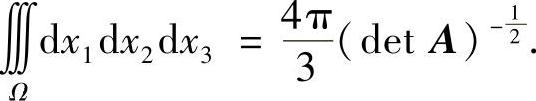
证明 因为A正定,所以存在正交矩阵T,使得
T′AT=diag(λ1,λ2,λ3),
其中λi>0(i=1,2,3)是A的特征根.记
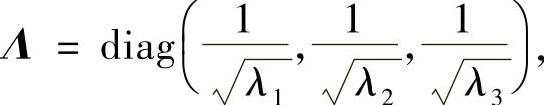
作变换
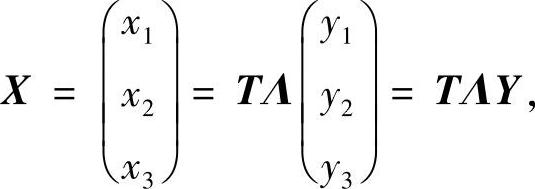
则变换的雅可比(Jacobi)行列式为
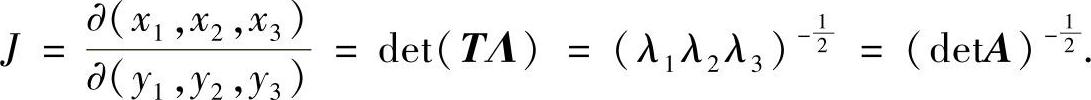
注意到
X′AX=(TΛY)′A(TΛY)=Y′Λ′T′ATΛY
=Y′Λ′(T′AT)ΛY=Y′Y,
有
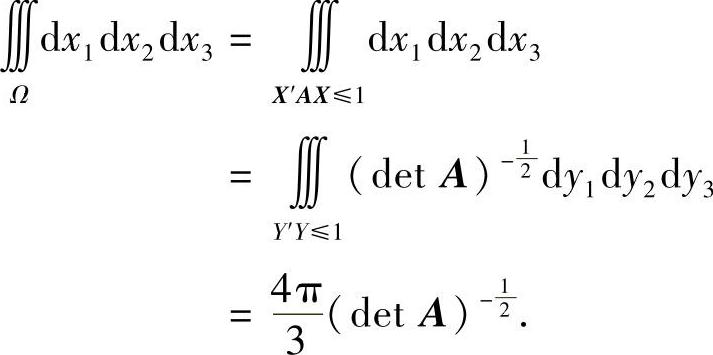
例7.44 计算下面的三重积分.
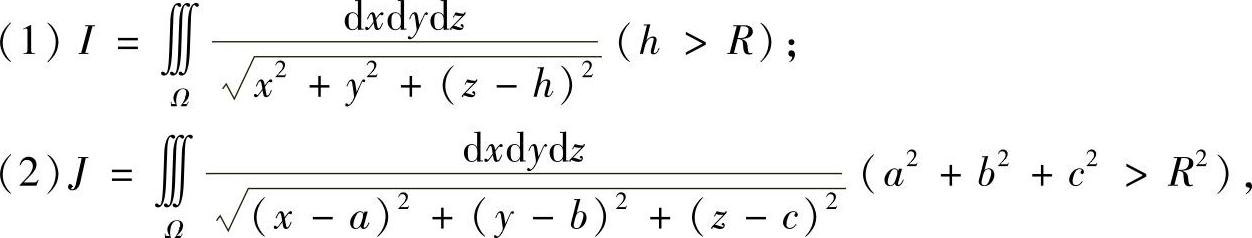
其中Ω:x2+y2+z2≤R2.
解(1)作柱坐标变换:x=rcosθ,y=rsinθ,z=z,则
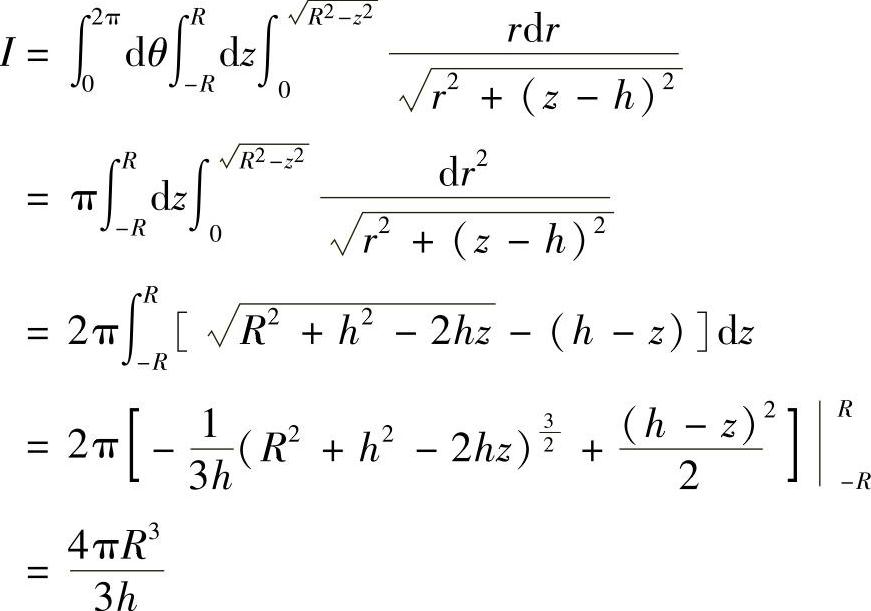
(2)作新坐标系Oξηζ,使ζ轴过点(a,b,c),且使坐标系Oξηζ到坐标系Oxyz之间的变换为正交变换(从坐标系Oξηζ→坐标系Oxyz可通过旋转变换来实现,因此从坐标系Oξηζ到坐标系Oxyz之间的正交变换是存在的!),变换的行列式为1.显然该变换将半径为R的球仍变为半径为R的球.记a2+b2+c2=h2,则由(1)知
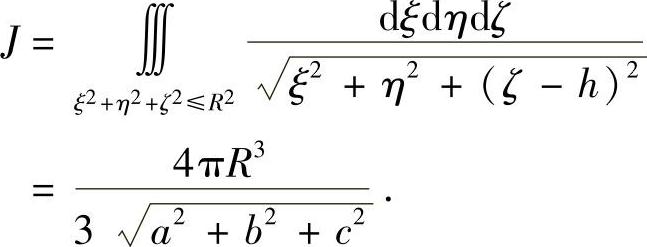
类题 设∑是单位球面x2+y2+z2=1,A是∑内部一点,它与原点的距离为q(0<q<1),ρ为点A与∑上的点之间的距离,求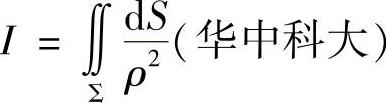 .
.
提示 设A点的坐标是(a,b,c),由题设条件,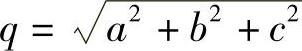 且0<q<1,而
且0<q<1,而
ρ2=(x-a)2+(y-b)2+(z-c)2,其中(x,y,z)∈Σ.
作坐标系的正交变换,使得A点位于新坐标系Oξηζ的ζ轴上,这样可以将积分I化成下面的形式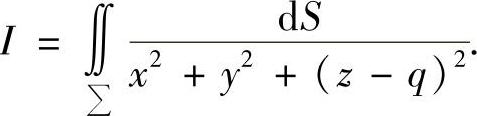
令x=cosθsinφ,y=sinθsinφ,z=cosφ,0≤θ≤2π,0≤φ≤π,通过计算可得dS=sinφdθdφ.于是
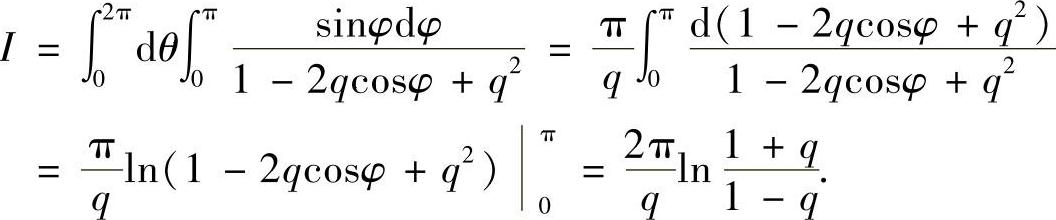
(6)广义重积分.
广义重积分在近年来各类学校的考题中出现的不多,尤其是证明题,但计算题中也曾出现过一些.广义重积分的计算大都也是通过化成累次积分甚至单积分来实现的,下面我们将通过例题来说明这一点.
比较判别法 设D是无界区域,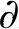 D是由有限段光滑或逐段光滑曲线所组成.函数f,g在D上有定义,对D的任一可求面积的有界子区域Dr,f,g均在Dr上有界可积.如果g非负,且
D是由有限段光滑或逐段光滑曲线所组成.函数f,g在D上有定义,对D的任一可求面积的有界子区域Dr,f,g均在Dr上有界可积.如果g非负,且
f(x,y)≤g(x,y), ∀(x,y)∈D,
则当g在D上(广义)可积时,f也在D上(广义)可积;
如果
f(x,y)≥g(x,y), ∀(x,y)∈D,
则当g在D上的广义积分发散时,f在D上的广义积分也发散.
记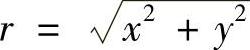 ,取
,取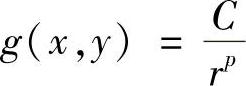 (C为常数),由上述比较判别法可得如下的
(C为常数),由上述比较判别法可得如下的
柯西判别法 对D,f的要求同上,则
(1)如果对充分大的r,有
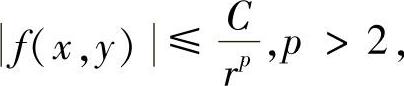
则广义积分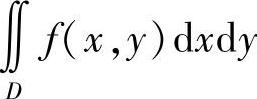 收敛;
收敛;
(2)如果D内含有一个顶点在原点的无限扇形:D′={(r,θ)r≥r0,α≤θ≤β},且在D′上,
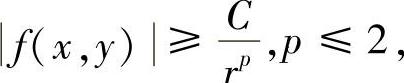
则广义积分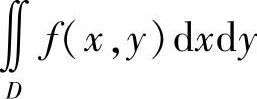 发散.
发散.
与一元函数在无限区间上的广义积分不同,广义重积分的收敛性与绝对收敛性等价.
对于无界函数在有界区域上的广义重积分可类似地讨论,在此不再赘述.
例7.45 计算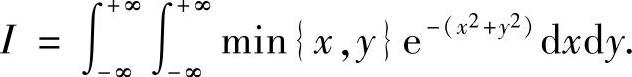
解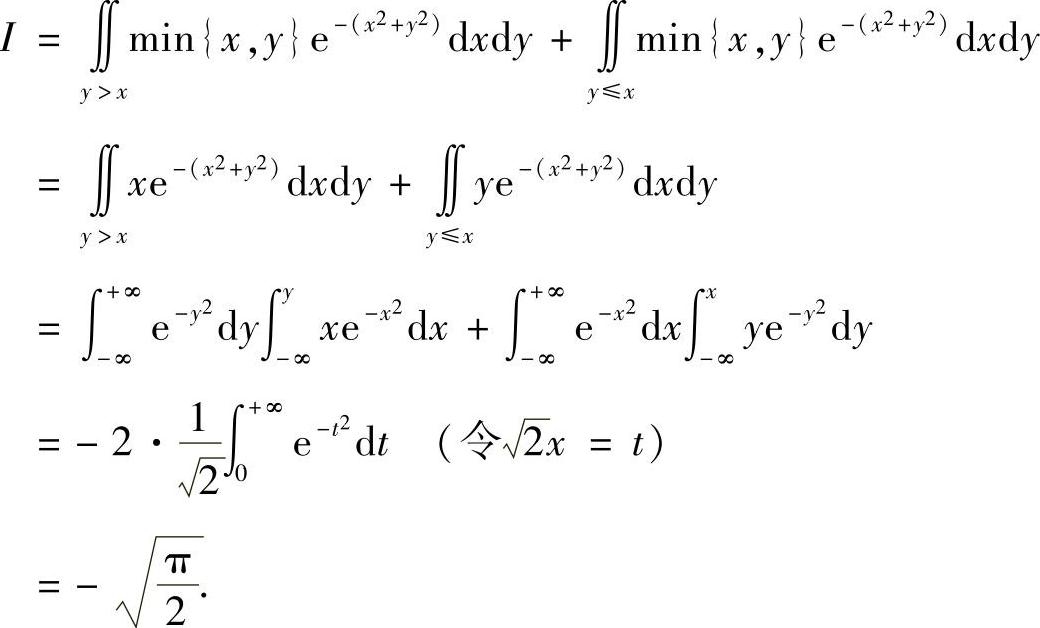
例7.46 讨论广义重积分
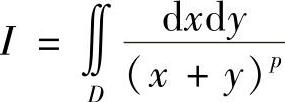
的敛散性,其中D={(x,y)0≤x≤1,x+y≥1}.当积分收敛时,求积分的值.
解 因为被积函数恒正,故可取Dr={(x,y)0≤x≤1,1≤x+y≤r},显然当r→+∞时,Dr趋于D.记
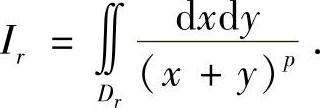
作变换:x=u,x+y=v,则
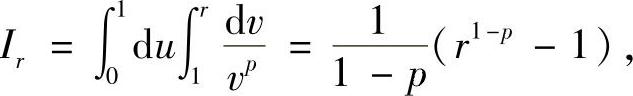
显然当p>1时,积分收敛,且积分值为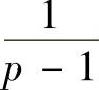 .
.
例7.47 讨论广义积分
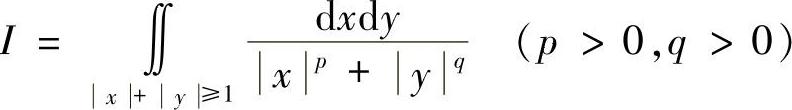
的敛散性.
解 由对称性,有
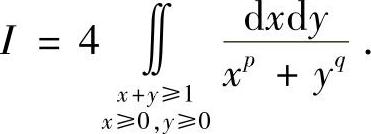
显然,I与下面的积分I′具有相同的敛散性,
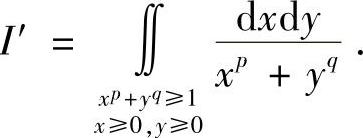
记Dr={(x,y)1≤xp+yq≤r2,x≥0,y≥0},显然当r→+∞时,Dr趋于区域D={(x,y)x+y≥1,x≥0,y≥0}.
下面考察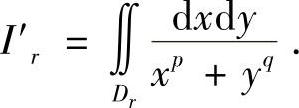
令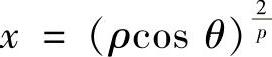 ,
,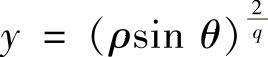 ,则
,则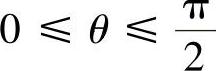 ,1≤ρ≤r,
,1≤ρ≤r,
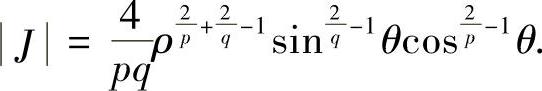
于是
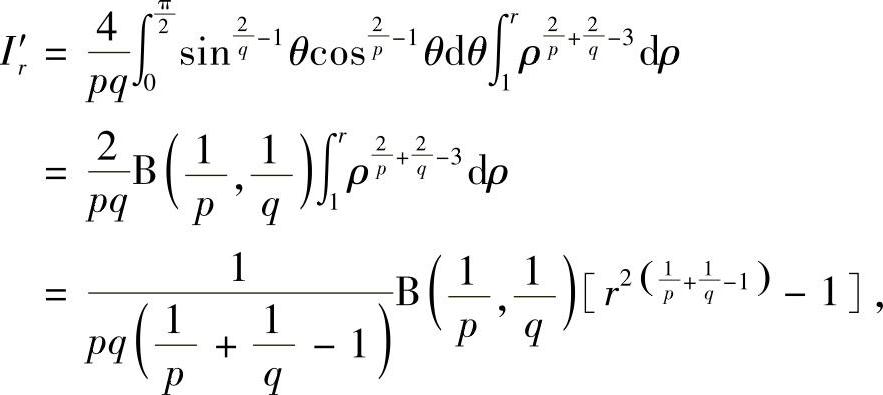
由此可见,当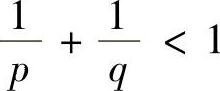 时积分收敛.
时积分收敛.
例7.48 计算广义三重积分
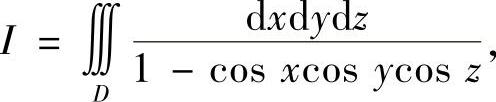
其中D为0<x<π,0<y<π,0<z<π.
解 作变换: ,
,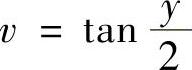 ,
,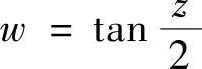 ,则0<u,v,w<+∞,
,则0<u,v,w<+∞,
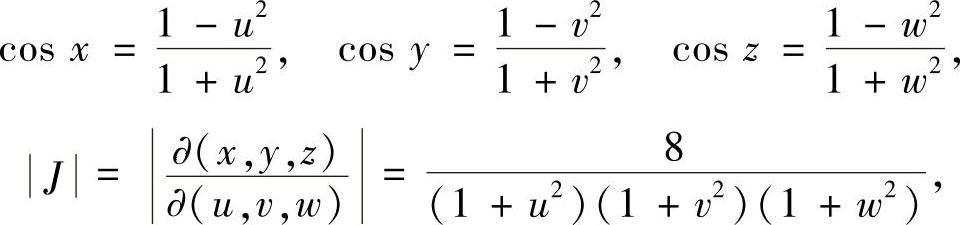
所以
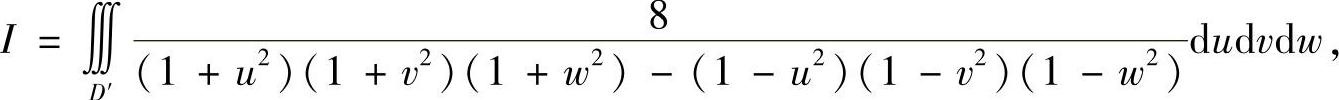
其中D′为u>0,v>0,w>0.
再作球坐标变换:u=rsinφcosθ,v=rsinφsinθ,w=rcosφ,则0<θ,
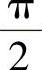 ,0<r<+∞,且J=r2sinφ.而
,0<r<+∞,且J=r2sinφ.而
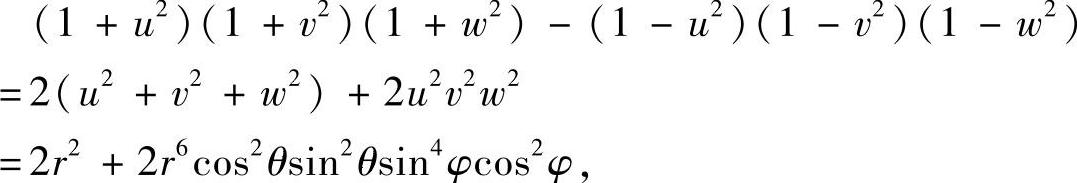
故
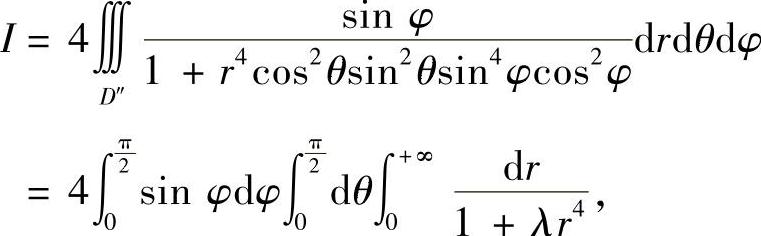
其中λ=cos2θsin2θsin4φcos2φ.由上式可见,积分是存在的,下面我们来计算它.
作变换:λr4=s,则
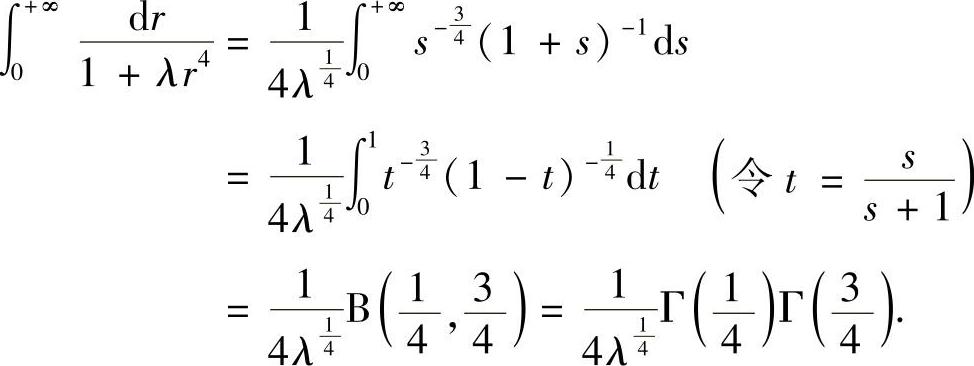
从而
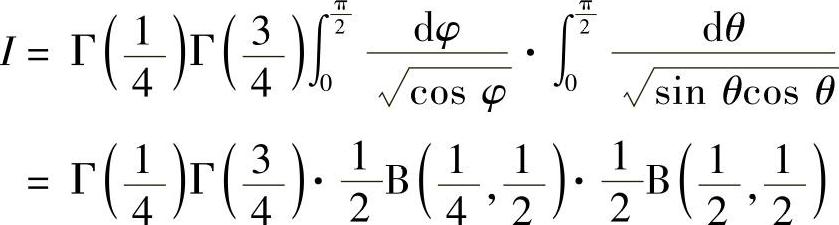
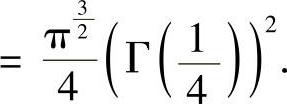
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




