中学数学课程发展研究:关于数学本质的探索

众多研究者将研究“什么是数学”看作是数学课程研究的核心之一.回答这个问题并非易事，我们首先应该明确回答问题的视角，是从数学哲学视角，还是从数学知识视角或者数学文化的视角来探讨.如果仅从数学哲学视角探讨“什么是数学”，也将得到不同的回答.数学家认为，不能简单地将数学看作是研究数及空间的科学，而是可以对此展开讨论和对话.

1.4.2.1　数学哲学的视角

傅种孙曾在1920年发表的论文“什么是数学”中评论国际上一些有关数学定义的说法，他分析到“近代数学中，有群论（theory of group），数理论理学（mathematical logic）等，既不依数，又不凭形，不能拿数及空间来范围它.”［57］同时，傅种孙以推崇的口吻介绍罗素的观点，即“数学是一门科学，里面讨论的对象没有指定，到底说什么是真也不知道”.^[1]傅先生评论说：“这个定义看起来似乎怪诞，其实意义很深远很宏大，确实可以代表近世数学的精义.”［58］数学是一门科学，但所研究的对象并不直接存在于现实世界.这是数学区别于其他学科的一个非常重要的特点.

吴文俊在《中国大百科全书·数学》中开宗明义地写道：“数学是研究现实世界中数量关系和空间形式的，简单地说，是研究数和形的科学.”尽管这是个权威的论断，但人们在研究中，对此有不同理解、补充和修改.现代数学的发展，已经超出“数”和“形”的范围，应当包括结构、范畴、模型等更广的对象.钱学森在《关于思维科学》一书中，把数学和哲学并列，认为数学是在社会科学和自然科学之上的一门学问.张奠宙和王善平所著《数学文化教程》则认为，关于数学的特点，一般都沿用亚历山大洛夫（A.D.Aleksandrov）的“三性”提法：抽象性、严谨性、广泛应用性.［59］

美国数学家和数学哲学家克莱因（M.Kline）指出，“数学本身就是一个充满活力的繁荣的文化分支.经过几千年的发展，数学已经成为一个宏大的思想体系，每个受过教育的人都应该熟悉其基本特征.”［60］在克莱因看来，数学主要是一种方法，它具体体现在数学的各个分支中，如关于实数的代数、欧氏几何，或任意的非欧几何.

克莱因指出，在很大程度上，数学提出了很多有关自身的问题.很多潜在可能的定理，就是通过对所观察的数以及几何图形加以总结得来的.例如，经常与整数打交道的人，会发现这一现象：前两个奇数之和，即1+3是2的平方；前3个奇数之和，即1+3+5是3的平方.类似地，前4，5，6个奇数之和也是如此.于是，通过这一简单的运算，就暗示着可能存在的一个普遍规律，即对任意一个自然数n，前n个奇数之和等于n的平方.一个有待证明的定理由此产生.而定理只能在经过一系列由公理出发的演绎推理确认为真之后才能成立.

数学方法本质就是它的抽象性.在自然界所提供的复杂经验中，数学抽象出某些特殊的方面并加以研究.这种抽象是为了减少所考察的事物的属性.例如，数学中的直线所具有的属性，通过一系列公理而得以表达出来，如两点确定一条直线.而现实中的直线除具有这一属性外，还有颜色，甚至有亮度和厚度.此外，现实中的直线都由具有复杂结构的分子所构成.数学具有强大威力的奥秘，部分地就存在于抽象之中.借助于这种抽象思维，可以摆脱烦琐的细节.克莱因以实验科学家为例，他指出，实验科学家因为基本上是直接与实物打交道，所以他们的思维就局限于由感官观察事物，从而束缚了手脚.数学家通过从事件中提取抽象的概念与属性，可以借助于抽象思维，而遨游于由视觉、声音、触觉等构成的物质世界之上.

克莱因认为，数学还可以处理诸如“能”这一类的物质，也许不能对它们进行定性的描述，因为它们超出了感觉世界的范围.例如数学能够解释万有引力，而万有引力作为宇宙的一种属性，是缥缈难测的.数学还能用来处理并揭示电、无线电、电磁波、光等种种神奇的现象.麦克斯韦（J.Maxwell）发现的电磁波与光波具有相同的微分方程规律，揭示出光波和电磁波具有同样的物理属性，这种联系在后来得到了无数次的证实.

英国数学家和哲学家怀特海（A.N.Whitehead）对此有着精辟论述：“没有什么比这一事实更令人难忘的了，数学脱离现实而进入抽象思维的最高层次，当它返回现实时，在对具体事实进行分析时，其重要性也相应增加了……最抽象的东西，是解决现实问题最有力的武器，这一悖论已完全为人们接受了.”［61］

1.4.2.2　数学的发现与发明

如果按照上述分析，数学被看作是关系结构，那么数学被看作是已存在的东西.按照柏拉图（Plato）的思想，数学也确实是存在于“思想天空”中，亚里士多德的观点则完全不一样，对他来说，人们在“建构”数学.因此按照柏拉图的思想，人们发现了数学；而按照亚里士多德观点，人们发明了数学.我们精确观察数学家的活动，这两个视角是不能分割的.即使人们假定，数学概念是被发明的，那么性质和关系是被研究发现的.

这一原理的讨论也有另一教育视角.人们可以这样提问：在学习已有知识时，人们是铭记知识还是建构知识，在教育研究中，有一段时间过于强调某个方面，而忽视另一个方面.但我们努力要做的是，在学校中看到这两个方面.

如果观察数学的产生，那么人们思想中首先出现的是某些基本观点，他们可以追溯到基本的数学概念上.然而，这不仅仅局限在某个在公理基础上构造的理论的“基本概念”上.

人们可以借助基本概念建构新的概念，这些可能是依照有限的条件产生的下位概念，但也算是新颖的、通过对偶而形成的概念.例如从自然数概念开始，根据限制条件“被2整除”，就获得“偶数”概念如果构造自然数对（m，n），就得到概念“分数”，由此书写出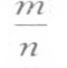当人们通过定义构造某个概念时，人们就会从性质以及和其他概念的关系角度探讨这个概念.探讨结果用“定理”描述出来.

另外，从数学史角度看数学问题，问题这个概念是开放的.例如，在欧几里得（Euclid）看来，构造的练习就是数学问题，其答案大部分直接来自假设、定理或者以及被解决的问题.基于理论以及已经给出和证明的结论，欧几里得为从问题导出常规问题寻找理由.当然希腊人也发现一些不能解决的问题.

古代最著名的是求圆积分（圆面积）问题.当初的问题是，只用圆规和直尺构造一个与圆面积一样大小的正方形.尽管，从欧氏几何角度看，四边形面积是个常规问题，但是几百年来找不到化圆为方的解法，直到1882年林德曼（F.Lindemann）证明了它的不可解性.

从数学史角度看，面积确定问题是基本问题的一条主线，当今也有新的问题，如分形几何问题.因此从数学史角度看，既有微观的问题又有较宏观的问题可以作为数学知识的源头.

当今人们对问题的理解是，有些问题没有明显的、直接可以找到的答案，人们还需要努力借助定理或者已经解决的问题来求得答案.如果人们解出来这个问题，并且这是个经常出现的问题类型，那么人们会编制一个算法，将解题过程图式化.

真实的数学教育，要求让学习者自己体验数学的产生，向他们传授一种手段，以便他们会自主地操作数学.在这种意义下，对应的专业目标是关于数学方法学习的目标.学生应该学会定义、猜想、证明、解决问题、编制算法或了解数学方法及其影响.这些专业目标也是一般课程目标的具体表现，如在一般课程目标中强调，用数学方法梳理数学外部和数学内部的情景，或者掌握关于数学知识等.

1.4.2.3　数学与现实

尽管数学发生在人类的思维中，但人们也努力在数学和他们能用感官感受的现实之间建立联系，也就是说，人们用“数学的眼睛”看现实.

如果人们对山的高度感兴趣的话，那么就设计将这座山与某个特定数对应起来，在此不考虑山的其他特征.这一数学兴趣限制了观察山的其他方面的视野，如果观察这座山的凸出部分，就能看到钝角上的尖尖.这个“数学视角”就这样向山里看去.

数学为观察者打开看待有趣关系的角度，但也限制他的视野，因此对世界的数学视角导致一个完全自己的世界观，人们可以逻辑地分析这两种视角.

忽视特定的特征，可以被看作为抽象，在数学中，构造概念时经常用到抽象.典型的例子是，集合的大小，在此人们不考虑元素的自然属性，仅仅关注数量这一特征；或者线段长度的例子，在此人们不考虑方位.但是概念可以被理想化，这里主要是指，人们看到这个对象里面去.例如，在运动中假设，路程和时间的关系是正比例关系，或者连接花园中两个点，称为线段.在数学教育中，要让学生意识到这种过程.(www.xing528.com)

数学也可以应用在非数学领域，用于解决问题.相反，外部的数学问题也能导致数学模型的产生，使得问题解决成为可能.真实的数学教育要让学习者意识到这种关系，并帮助他们，操作相应的技术.学生应该：学会应用数学、学会创建数学模型.

数学与现实世界之间的关系也会受到学生的质疑，数和形的世界尽管与某些“真实生活”有联系，但是这个世界要遵循自己的规则，而这些规则又与“常人的理解”不很吻合.例如学生能接受“所有”这个概念，但是也有不实际的结果，如0.75只狗，或者5米高的人在数学世界中是可能的.又如，尽管3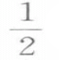个人看起来是很不合理的量，但是也会得到正确的结果.当学生得出非整数时，学生会产生怀疑，并开始寻找错误.如果这个问题的设计，确实要得出一个非整数，那么学生会很困惑.为了避免这种错误的感觉，要求数学课程接近生活，也就是说，要让学生处理真正的情景和真实的数据.对于数学课程的这类真实性的要求，人们自然会疑惑，学生在这样的学习期间是否会获得可靠的数学经验.

1.4.2.4　数学观的形成

通过数学课程学生形成各种可能的数学观，研究者列举如下数学观：［62］

（1）数学是关于数和图形的学科；

（2）数的特征被作为规则描述出来，图形的特征被作为定理描述出来；

（3）规则和定理是可证明的；

（4）依据规则和定理，可以解决特定的问题；

（5）每个习题（问题）有一个解决的范式（图式）；

（6）数学是一直存在的；

（7）数学中没什么新的东西；

（8）数学需要一种特殊的才能；

（9）数学是让男生学的学科，而不是给女生的学科.

从上面列出的数学观可见，通过数学课程而形成的数学观有的比较合理，有的则让数学家感觉到不舒服，因为有些纯粹是偏见.当我们回望中学阶段学生所面对的数学课程，大部分是数学定义、定理的学习，以及严谨的数学证明的训练，学生对数学的朴实的认识受到质疑，渐渐地学生习惯这种数学，数学观也就僵化在如下方面：

（1）数学是关于结构的科学；

（2）关于各种不同的结构的知识体现在理论中；

（3）理论是建立在公理之上的；

（4）数学是扎根在数和图形之中的，但也在不断发展；

（5）尽管数学能让人有创造性，但真正要发现新的东西，还是需要特别的天赋，这种天赋只有很少人拥有.

许多教师在自己学业阶段拥有这种数学观，因此在教学过程中，不经意地表露出这种观念，尽管他们从发生论的角度，尝试让学生从历史发展的角度，了解数学的生成过程，但仅仅是表面的，而无法与学生进行深层次的数学史的交流，因为教师自身在教育阶段没有经历数学史的课程.

1.4.2.5　对数学的态度

数学陪伴着学生度过整个学校学业生涯.在这过程中，不少学生从数学学习中获得乐趣，但还是有学生在数学上受到挫折或者打击.数学有着迷人的特征，会让人沉迷于计算、推理中，沉浸于问题分析和解决中.几何中的直观图形以及非常规图形也吸引着不少人的思维或动手操作.但是数学在带给人成就的同时，也要求人们学会纠正错误.

研究表明，教师可以帮助学生转变对数学的态度，尤其是那些自身喜欢数学、喜欢学生，又有一定的教育理念的教师.这里就涉及如何唤醒学生数学兴趣的话题.如果能让学生经历“另一种数学课程与教学”，那么学生会为之而惊讶，原来数学也可以这样有趣.德国教育家瓦根舍因（M.Wagenschein）曾经引用学生的一封信，在这封信里学生描述了自己找到质数数列的不可中断性后的那种感觉：“她没有想到会如此激动.我们根本没有去想……数学对我来说一直是无聊的代名词，我几乎不敢相信，这种愉悦的经历居然也可以称为数学……当我们几天后解出这个问题后，我们非常自豪，这个质数数列问题折磨着我们的人生，只有到找到答案后，发现我们做回了人.”［63］