运动副的限制与约束如何影响构件自由运动？

构件在平面XOY坐标内做平面运动时，它可以有3个独立的运动，既可以沿X轴方向移动，也可以沿Y轴方向移动，还可以在XOY平面内转动。把构件在平面内的这种独立运动，称为构件的活动度。构件这时有3个活动度。换言之，所谓构件的活动度，也就是确定构件位置时所需要的独立参数的数目。

平面低副限制或取消构件的两个活动度，或者说它产生了两个约束条件。

平面高副限制或取消构件的一个活动度而保留了两个活动度，或者说它产生了一个约束条件。

1.机构具有确定运动的条件

我们把确定一个机构位置所需要的独立参数的数目称为机构的活动度，把给定运动规律的杆件称为原动件，而把除原动件以外的杆件称为从动件。得出结论如下：

要使一个机构具有确定运动，则必须使机构的原动件数等于机构的活动度数。这就是机构具有确定运动的条件。显然，若原动件数少于机构的活动度数，则机构的运动将不确定；相反，若原动件数大于机构的活动度数，则因独立运动过多，而使机构中的最弱构件遭到破坏。

平面机构活动度的计算方法：

在设计新的机构或分析一个现有的机构是否能运动，以及应该给定几个原动件，机构才能有确定的运动时，首先就要判断机构的活动度是多少。机构活动度的判断可以用直接观察分析的方法，也可以用公式计算。计算平面机构活动度的方法如下：

当一个自由构件做平面运动时，它具有3个活动度。如果一个机构里有n个可动的构件，则构件的总的活动度数应为3n个。当这些构件分别用运动副将它们连接后，构件间的相对运动就受到了约束，也即它们的自由运动受到了限制，活动度数相应减少。活动度减少的数量与运动副的性质及数目有关，如组成机构时形成Pd个低副（转动副或移动副），因为每个低副限制两个活动度，则该机构就失去2Pd个活动度。如在此机构中尚有Pg个高副，因为每个高副限制一个活动度，因此机构又失去1×Pg个活动度。这样，这个机构共失去的活动度数为（2Pd+Pg）个，此时机构还剩的活动度数（即机构的活动度数）W应为

W=3n-2Pd-Pg

此即所谓的机构的结构公式。

2.特殊问题

在用上述公式计算平面机构的活动度时，有时会遇到按公式计算出的活动度数与实际活动度数不相符的情况，这并不是公式本身有错误，而是运用这个公式时忽视了机构结构中的某些特殊情况。分述如下：

（1）复合铰链

图3-73a所示为一摇筛机构，构件2、3分别与构件4组成转动副，如图3-73b所示。当用公式计算该机构的活动度时，往往容易把它当作一个转动副来计算，而使得出的机构活动度数与实际的情况不符。例如，往往容易把该机构的转动副和移动副的总数算为6，结果得出机构的活动度数为

图3-73 摇筛机构运动简图

W=3n-2Pd-Pg=3×5-2×6-0=3

这表示要使该机构具有确定运动，需要给出3个原动件。但实际上只要驱动偏心轮1，机构就具有确定运动。这一错误的发生是由于没有把铰链C处的转动副按实际情况算为两个，如图3-73b所示，而只算了一个。如按实际情况算为两个，则转动副和移动副的总数就不是6而是7，这样机构的活动度数为

W=3n-2Pd-Pg=3×5-2×7-0=1

与实际情况相符。所以铰链C称为复合铰链。当我们遇到由m个构件组成的复合铰链时，其运动副的数目应为（m-1）个。

（2）局部自由度

图3-74a为一滚子推杆凸轮机构，它与图3-74c所示的凸轮机构的不同之处在于推杆的头部装有一个能够转动的圆滚子，以减轻推杆与凸轮轮廓之间的磨损。用公式计算该机构的活动度：

活动构件数 n=3

低副数 Pd=3

高副数 Pg=1

机构的活动度数 W=3n-2Pd-Pg=3×3-2×3-1=2

但实际上该机构的活动度为1，也即只要给凸轮1以确定运动后，则推杆2的运动就完全确定。为何计算所得与实际情况不符呢？原来在该机构中，有的构件的运动对整个机构并没有什么影响，如滚子3只绕自身的几何轴心转动，并不影响推杆2的运动规律，其作用与图3-74b完全相同。这种不影响整个机构运动特性的自由度，称为局部自由度或多余自由度。在计算机构的活动度时，应把这种局部自由度除去，方能得出正确的结果。例如在计算时除去滚子的自由度后，机构的活动度为

图3-74 带有局部自由度的机构

W=3n-2Pd-Pg=3×2-2×2-1=1，与实际情况相符。

（3）虚约束

图3-75a为一机车车轮连动机构，该机构的特点是AB、CD、EF三杆件长度相等且相互平行，BF和AE长度相等也相互平行。按公式计算机构的活动度，由图可知：

图3-75 带有虚约束的联动机构

活动构件数 n=4

低副数 Pd=6

高副数 Pg=0

机构活动度 W=3n-2Pd-Pg=3×4-2×6-0=0

表示该机构不能动。但实际上该机构是可以运动的，只要给机构中某一构件以确定运动，则其余各构件均能做有规律的运动。用公式计算的结果为什么与实际情况不相符合呢？原来由于该机构中各杆长度相等且相互平行，当杆件AB绕A点回转时，杆件CD和EF分别绕C、E点回转，连杆BF做平移运动，其上各点的轨迹都是圆，D点的轨迹是以C为中心的圆。如将CD杆除去，则连杆BF的运动不变，连杆上D点的轨迹也不变。可见，CD杆加到该机构上去的两个运动副C和D并没有起到新的约束作用，或者说它们所起的约束作用是与AB杆及EF杆加到机构上去的运动副所起的作用是相重复的，这种对运动不起任何影响的约束，称为虚约束或重复约束。当计算机构的活动度时，应把这种虚约束除去，如将该机构中的CD杆除去，则剩下的就是四杆机构，其活动度为W=3n-2Pd-Pg=3×3-2×4-0=1。

计算结果与实际情况相符合。

如果杆件CD与杆件AB、EF不相等且不平行，如图3-75b所示，此时C、D这两个运动副将对机构的运动起限制作用，也即它们不再是虚约束而是真约束。显然，此时机构的活动度为零，实际上不可能运动，而是成了一刚性构架。

图3-76所示为一对外啮合圆柱齿轮机构，用公式计算其活动度，由图可知：

活动件数 n=2

低副数 Pd=4

高副数 Pg=1

机构活动度 W=3n-2Pd-Pg=3×2-2×4-1×1=-3

表示该机构不能运动，但实际上该机构是能够运动的。计算结果与实际情况不符，是由于4个轴承中实际上起约束作用的只有两个，即A、B中有一个，C、D中有一个，其他两个是虚约束。把它们除去后，则机构的活动度为

W=3n-2Pd-Pg=3×2-2×2-1×1=1

计算结果与实际相符。

虚约束对机构的运动是没有影响的，但它可以用来改善机构的受力状况。另外，当机构运动处在死点位置时，还可以利用虚约束来克服机构运动的不确定性，从而保证其运动规律。图3-77所示为一平行四杆机构，为了保证在机构运动的过程中，当杆件AB、BC、CD处于一直线时，不致形成反平行四杆机构，加上了EF这一辅助杆件，即加上了虚约束。

（4）铰链四杆机构

全部用回转副组成的平面四杆机构称为铰链四杆机构，如图3-78所示。

图3-76 带有虚约束的外啮合圆柱齿轮机构

图3-77 带有虚约束的平行四边形四杆机构

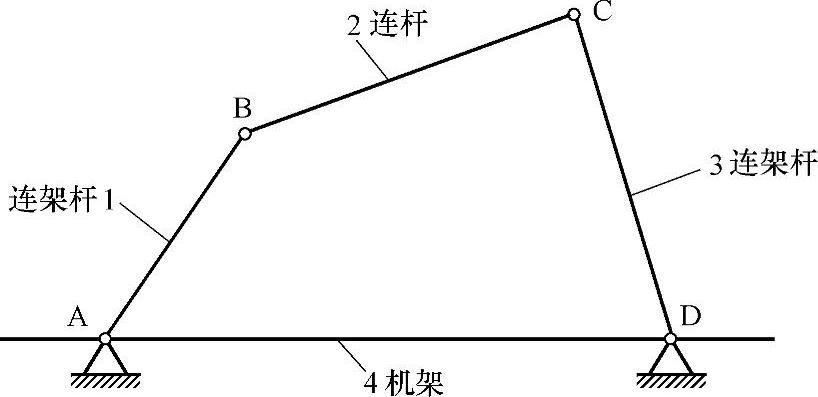
图3-78 铰链四杆机构

图3-78中，机构的固定杆4称为机架，与机架用回转副相连接的杆1和杆3称为连架杆，不与机架直接连接的杆2称为连杆。能做整周转动的连架杆，称为曲柄。仅能在某一角度摆动的连架杆，称为摇杆。

对于铰链四杆机构，机架和连杆总是存在的，因此可按照连架杆是曲柄还是摇杆，将铰链四杆机构分为三种基本型式：

曲柄摇杆机构、双曲柄机构和双摇杆机构。

1）曲柄摇杆机构：在铰链四杆机构中，若两个连架杆，一个为曲柄，另一个为摇杆，则此铰链四杆机构称为曲柄摇杆机构。曲柄摇杆机构的主要特性有：

a.急回运动

图3-79所示为一曲柄摇杆机构，其曲柄AB在转动一周的过程中，有两次与连杆BC共线。在这两个位置，铰链中心A与C之间的距离AC₁和AC₂分别为最短和最长，因而摇杆CD的位置C₁D和C₂D分别为其两个极限位置。摇杆在两极限位置间的夹角ψ称为摇杆的摆角。

当曲柄由AB₁顺时针转到AB₂时，曲柄转角φ₁=180°+θ，这时摇杆由C₁D摆到C₂D，摆角为ψ；而当曲柄顺时针再转过角度φ₂=180°-θ时，摇杆由C₂D摆回C₁D，其摆角仍然是ψ。虽然摇杆来回摆动的摆角相同，但对应的曲柄转角不等（φ₁>φ₂）。当曲柄匀速转动时，对应的时间也不等（t₁>t₂），从而反映了摇杆往复摆动的快慢不同。令摇杆自C₁D摆至C₂D为工作行程，这时铰链C的平均速度是v₁=C₁C₂/t₁；摆杆自C₂D摆回至C₁D为空回行程，这时C点的平均速度是v₂=C₁C₂/t₂，v₁<v₂，表明摇杆具有急回运动的特性。急回特性可用行程速比系数K表示，即

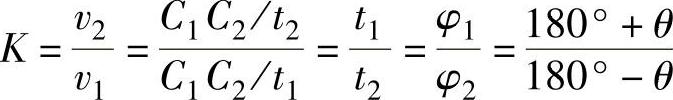
整理后，可得极位夹角的计算公式

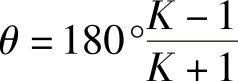
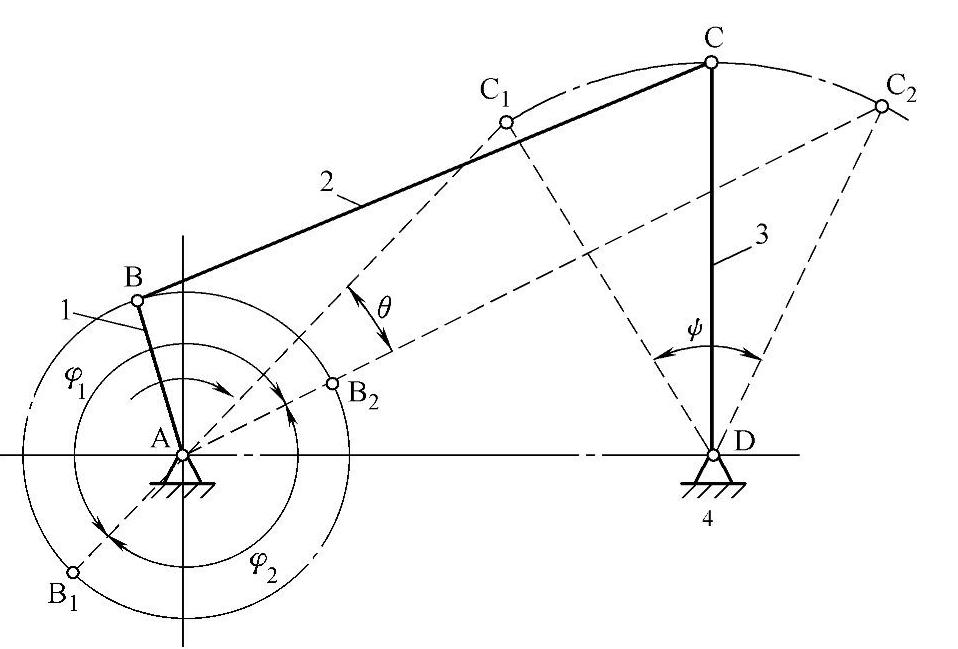
图3-79曲柄摇杆机构的急回特性

b.压力角和传动角

在生产实际中往往要求连杆机构不仅能实现预期的运动规律，而且希望运转轻便、效率高。图3-80所示的曲柄摇杆机构，如不计各杆质量和运动副中的摩擦，则连杆BC为二力杆，它作用于从动摇杆3上的力P是沿BC方向的。作用在从动件上的驱动力P与该力作用点绝对速度v_c之间所夹的锐角α称为压力角。由图3-80可见，力P在v_c方向的有效分力为P_t=Pcosα。

它可使从动件产生有效的回转力矩，显然P_t越大越好。而P在垂直于v_c方向的分力P_n=Psinα则为无效分力，它不仅无助于从动件的转动，反而增加了从动件转动时的摩擦阻力矩。因此，希望P_n越小越好。由此可知，压力角α越小，机构的传力性能越好，理想情况是α=0，所以压力角是反映机构传力效果好坏的一个重要参数。一般设计机构时都必须注意控制最大压力角不超过许用值。

图3-80 压力角与传动角

在实际应用中，为度量方便起见，常用压力角的余角γ来衡量机构传力性能的好坏，γ称为传力角。显然，γ值越大越好，理想情况是γ=90°。

一般机械中，[γ]=40°～50°。大功率机构，γ_min=[γ]≥50°。

非传动机构，[γ]<40°，但不能过小。

确定最小传动角γ_min。由图3-80中△ABD和△BCD可分别写出

（BD）2=l²₁+l₄²-2l₁l₄cosφ

（BD）2=l²₂+l²₃-2l₂l₃cos∠BCD

由此可得

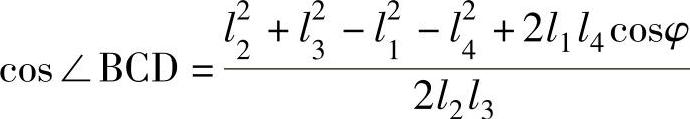
当φ=0和180°时，cosφ=+1和-1，∠BCD分别最小和最大（见图3-80）。

当∠BCD为锐角时，传动角γ=∠BCD，是传动角的最小值，也即∠BCD（min）。

当∠BCD为钝角时，传动角γ=180°-∠BCD，∠BCD（max）对应传动角的另一极小值。

若∠BCD由锐角变钝角，机构运动将在∠BCD（min）和∠BCD（max）位置两次出现传动角的极小值。两者中较小的一个即为该机构的最小传动角γ_min。

c.死点

对于图3-80所示的曲柄摇杆机构，如以摇杆3为原动件，而曲柄1为从动件，则当摇杆摆到极限位置C₁D和C₂D时，连杆2与曲柄1共线，若不计各杆的质量，则这时连杆加给曲柄的力将通过铰链中心A，即机构处于压力角α=90°（传力角γ=0）的位置时，驱动力的有效力为0。此力对A点不产生力矩，因此不能使曲柄转动。机构的这种位置称为死点。死点会使机构的从动件出现卡死或运动不确定的现象。可以利用回转机构的惯性或添加辅助机构来克服。

有时利用死点来实现工作，如图3-81所示工件夹紧装置，就是利用连杆BC与摇杆CD形成的死点，这时工件经杆1、杆2传给杆3的力，通过杆3的传动中心D。此力不能驱使杆3转动。故当撤去主动外力F后，工件依然被可靠地夹紧。

2）双曲柄机构：两连架杆均为曲柄的铰链四杆机构称为双曲柄机构。双曲柄机构中，用得最多的是平行双曲柄机构，或称平行四边形机构，它的连杆与机架的长度相等，且两曲柄的转向相同，长度也相等。由于这种机构两曲柄的角速度始终保持相等，且连杆始终做平动，故应用较广。当4个铰链中心处于同一直线如图3-82a所示时，将出现运动不确定状态。例如在图3-82b中，当曲柄1由AB₂转到AB₃时，从动曲柄3可能转到DC₃′，也可能转到DC″₃。为了消除这种运动不确定现象，除可利用错列机构（见图3-82b），还可利用从动件本身或其上的飞轮惯性导向，或辅助曲柄等措施来解决。如图3-83所示的机车驱动轮联动机构，就是利用第三个平行曲柄（辅助曲柄）来消除平行四边形机构在这种位置运动时的不确定状态。

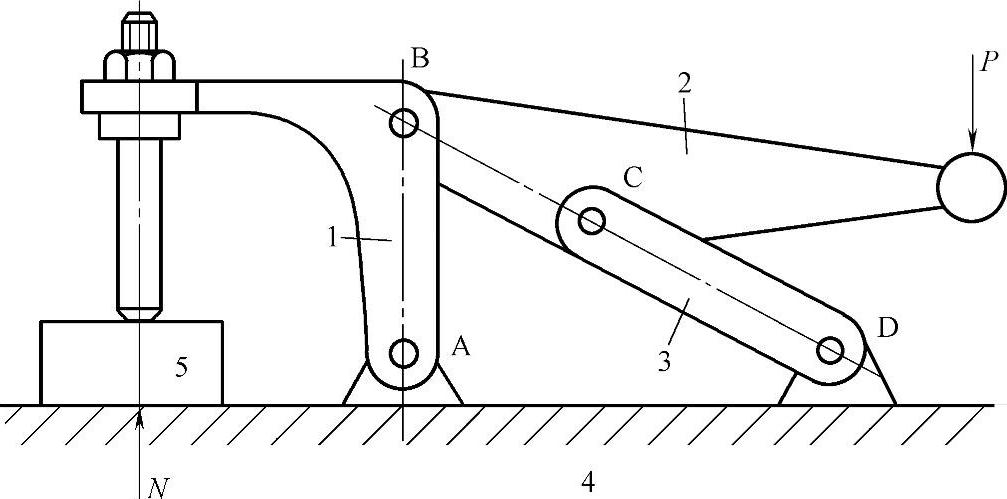
图3-81 利用死点夹紧工件的夹具

3）双摇杆机构：两连架杆均为摇杆的铰链四杆机构称为双摇杆机构。两摇杆长度相等的双摇杆机构，称为等腰梯形机构。

3.铰链四杆机构的演化

（1）铰链四杆机构的曲柄存在条件

铰链四杆机构中是否存在曲柄，取决于机构各杆的相对长度和机架的选择。如图3-84所示的机构中，杆1为曲柄，杆2为连杆，杆3为摇杆，杆4为机架，各杆长度以l₁、l₂、l₃、l₄表示。为了保证曲柄1整周回转，曲柄1必须能顺利通过与机架4共线的两个位置AB′和AB″。

当曲柄处于AB′时，形成三角形B′C′D。根据三角形两边之和必大于第三边，可得

图3-82a 平行四边形机构及其不确定性

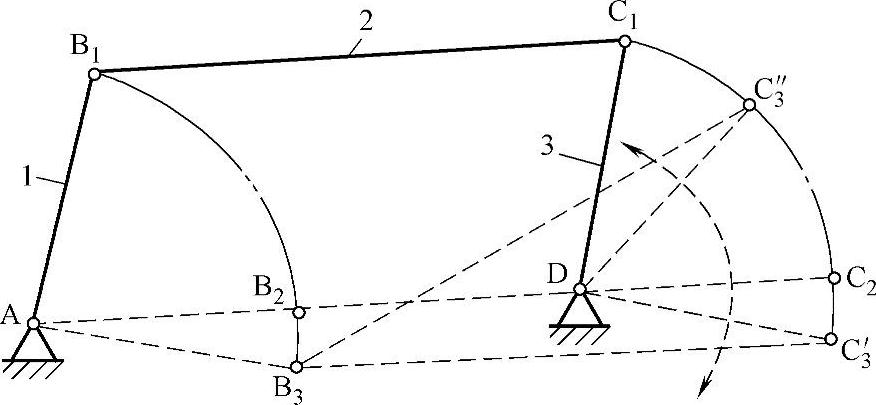
图3-82b 利用错列机构克服平行四边形机构不确定性状态

l₂≤（l₄-l₁）+l₃

l₃≤（l₄-l₁）+l₂即：

l₁+l₂≤l₃+l₄

l₁+l₃≤l₂+l₄

当曲柄处于AB″位置时，形成三角形B″C″D。可写出以下关系式：

l₁+l₄≤l₂+l₃

将以上三式两两相加可得

l₁≤l₂l₁≤l₃l₁≤l₄

上述关系说明曲柄存在的必要条件是：

1）在曲柄摇杆机构中，曲柄是最短杆；

2）最短杆与最长杆长度之和小于或等于其余两杆长度之和。

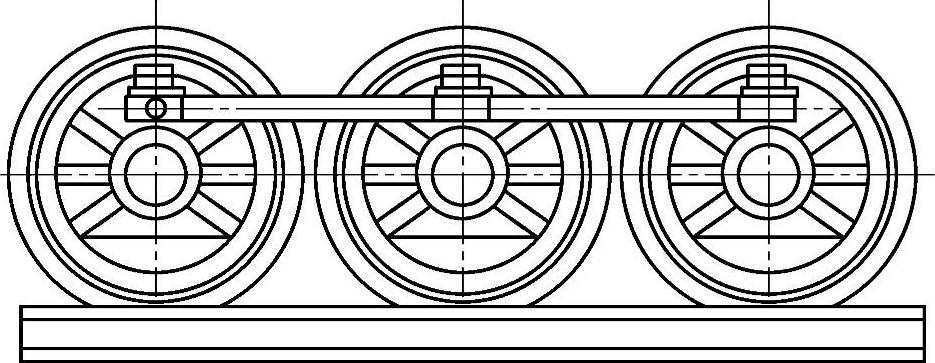
图3-83 机车驱动轮联动机构

（2）如何得到不同类型的铰链四杆机构

根据以上分析可知：

当各杆长度不变时，取不同杆为机架就可以得到不同类型的铰链四杆机构。

1）取最短杆相邻的构件（杆2或杆4）为机架时：最短杆1为曲柄，而另一连架杆3为摇杆，如图3-85a所示的两个机构均为曲柄摇杆机构。

2）取最短杆为机架时：其连架杆2和4均为曲柄，如图3-85b所示为双曲柄机构。

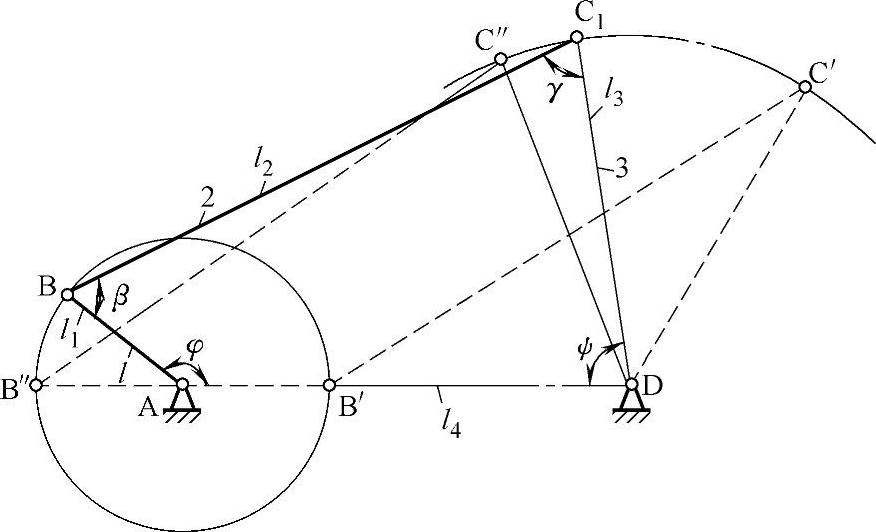
图3-84 曲柄存在的条件分析

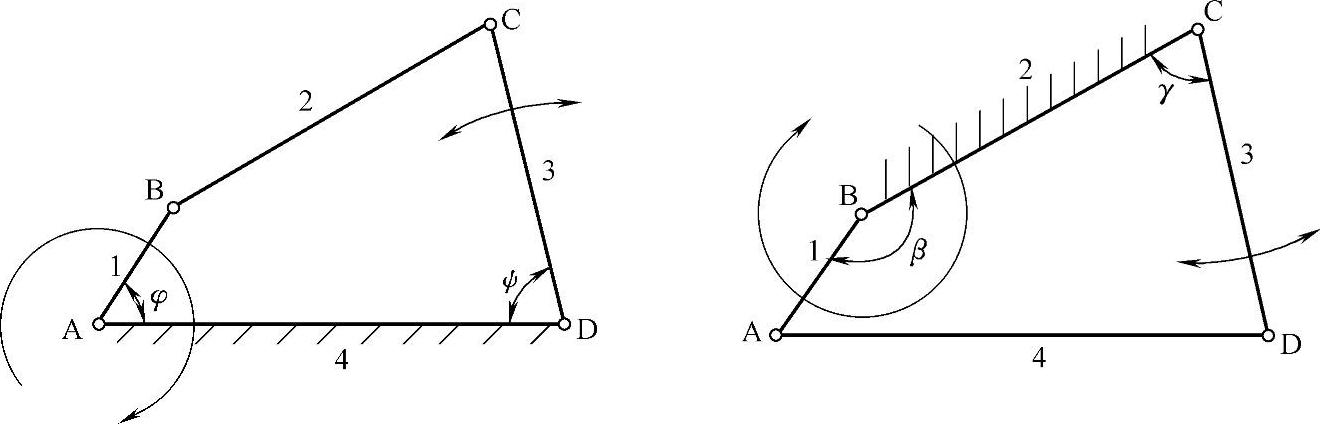
图3-85a 最短杆相邻的构件（杆2或杆4）为机架→曲柄摇杆机构

3）取最短杆的对边（杆3）为机架时：两连架杆2和4都不能整周转动，如图3-85c所示为双摇杆机构。

由上述分析可知：

最短杆和最长杆长度之和小于或等于其余两杆长度之和是铰链四杆机构存在曲柄的必要条件。满足这个条件的机构究竟有一个曲柄、两个曲柄或没有曲柄，还需根据取何杆为机架来判断。

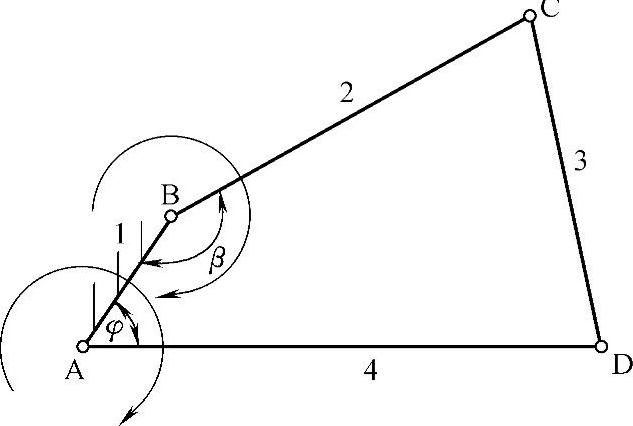
图3-85b 最短杆为机架→双曲柄机构

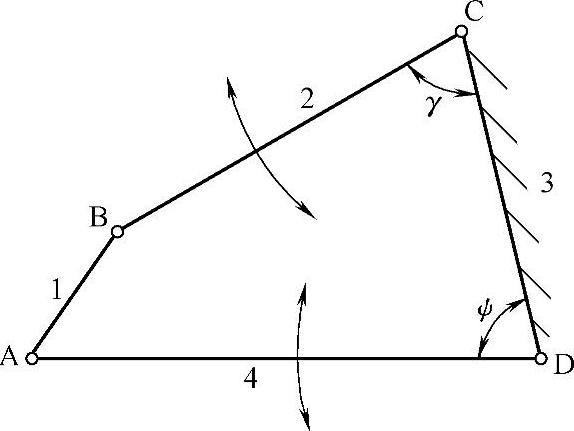
图3-85c 最短杆的对边（杆3）为机架→双摇杆机构

（3）铰链四杆机构的演化

1）曲柄滑块机构：图3-86a所示的曲柄摇杆机构中，摇杆3上C点的轨迹是以D为圆心，以杆3的长度l₃为半径的圆弧。如将转动副D扩大，使其半径等于l₃，并在机架上按C点的近似轨迹作成一弧形槽，摇杆3作成与弧形槽相配的弧形块，如图3-86b所示。

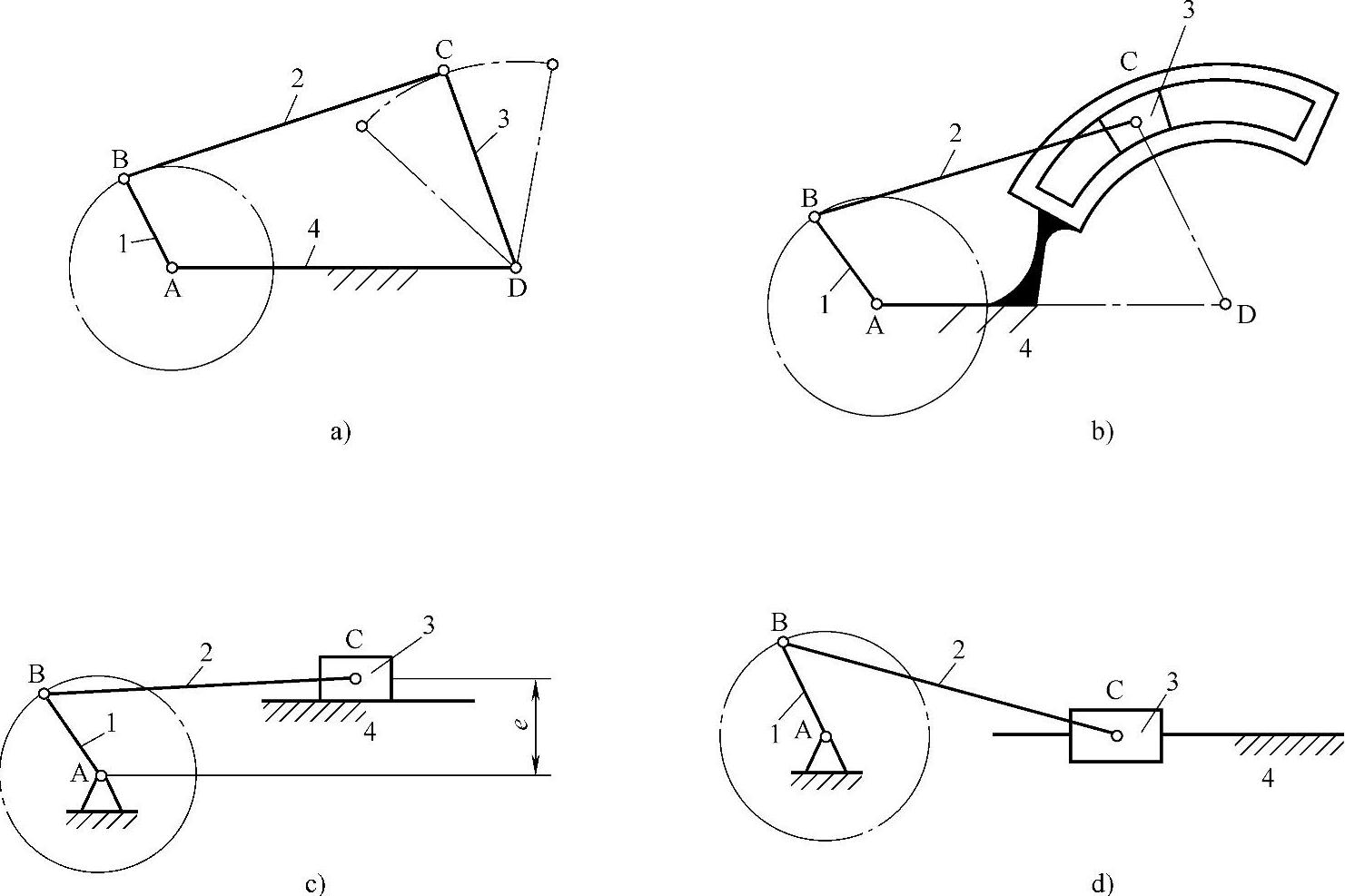
图3-86 曲柄滑块机构的演化

若将弧形槽的半径增至无穷大，则转动副D的中心移至无穷远处，弧形槽变为直槽，转动副D则转化为移动副，构件3由摇杆变成了滑块，于是曲柄摇杆机构就演化为曲柄滑块机构，如图3-86c所示。此时，移动方位线不通过曲柄回转中心，故称为偏置曲柄滑块机构。曲柄转动中心至其移动方位线的垂直距离称为偏距e。当移动方位线通过曲柄转动中心A时（即e=0），则称为对心曲柄滑块机构，如图3-86d所示。

2）导杆机构：图3-87a所示为曲柄滑块机构。若取曲柄为机架，则演变为导杆机构，如图3-87b所示。若AB<BC，则杆2和杆4均可做整周回转，故称为转动导杆机构。若AB>BC，则杆4均只能做往复摆动，故称为摆动导杆机构。

3）摇块机构：若取杆2为固定件，即可得图3-87c所示的摆动滑块机构，或称摇块机构。

4）定块机构：若取杆3为固定件，即可得图3-87d所示的固定滑块机构或称定块机构。

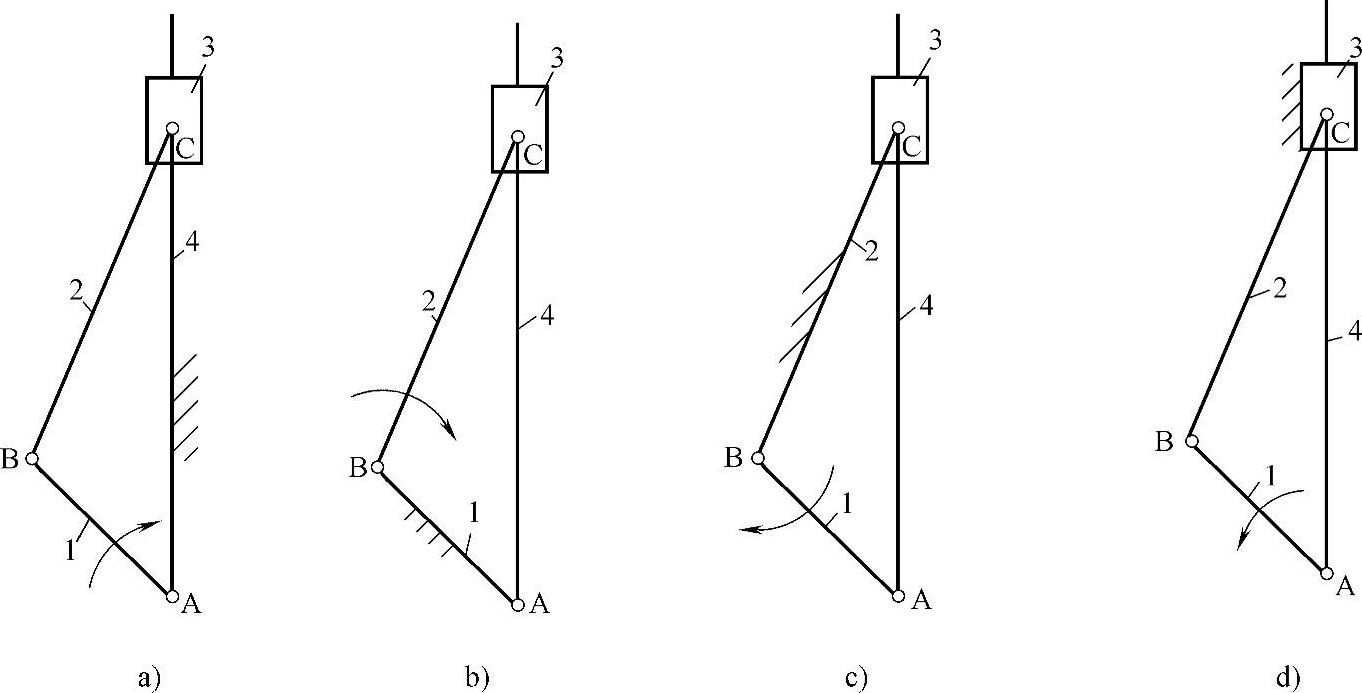
图3-87 导杆机构、摇块机构和固定滑块机构

5）双滑块机构：曲柄滑块机构演化为具有两个移动副的四杆机构，称为双滑块机构。在图3-88a所示的曲柄滑块机构中，将转动副B扩大，则图3-88a所示的曲柄滑块机构，可等效为图3-88b所示的机构。将圆弧槽mm的半径逐渐增至无穷大，则图3-88b所示机构就演化为图3-88c所示的机构。此时连杆2转化为沿直线mm移动的滑块2，转动副c则变成为移动副，滑块3转化为移动导杆。

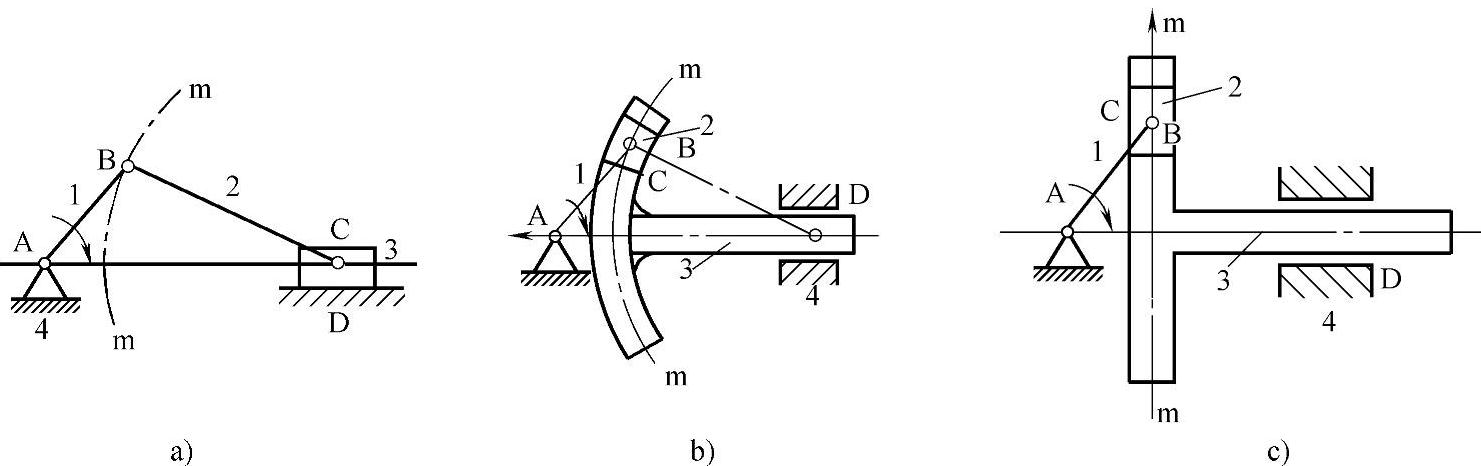
图3-88 曲柄移动导杆机构

①两个移动副不相邻，如图3-89所示。这种机构的从动件3的位移与原动件转角的正切成正比，故称为正切机构。

②两个移动副相邻，且其中一个移动副与机架相关联，如图3-90所示。这种机构的从动件3的位移与原动件转角的正弦成正比，故称为正弦机构。

③两个移动副都与机架相关联，图3-91所示的椭圆仪就是这种机构的例子。当滑块1和3沿机架的十字槽滑动时，连杆2上的各点便描绘出长、短不同的椭圆。

4.平面四杆机构的设计

平面四杆机构的设计是指根据工作要求选定机构的型式，根据给定的运动要求确定机构的几何尺寸。其设计方法有作图法、解析法和实验法。作图法比较直观；解析法比较精确；实验法常需试凑。

（1）作图法

1）按照给定连杆的几个位置设计，如图3-92所示。

图3-89 正切机构

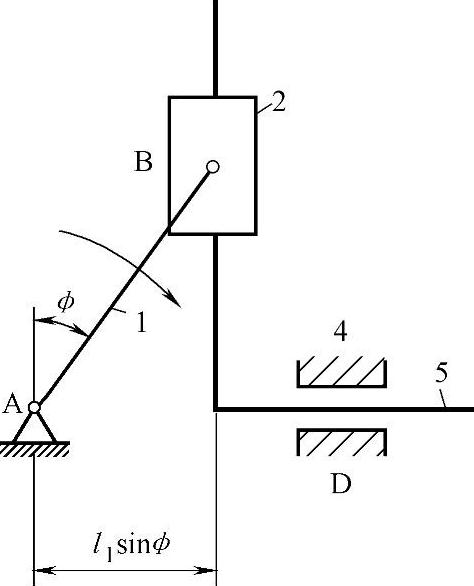
图3-90 正弦机构

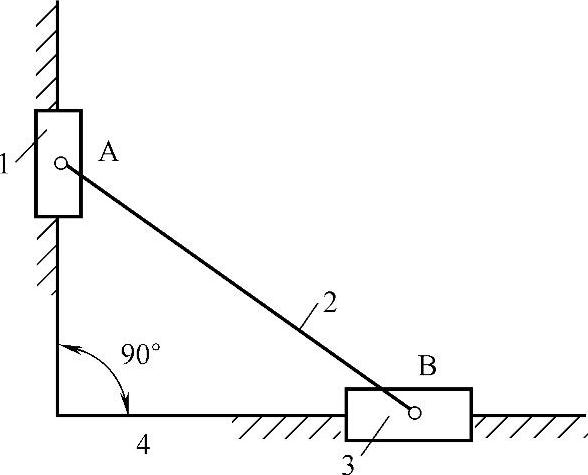
图3-91 椭圆仪机构

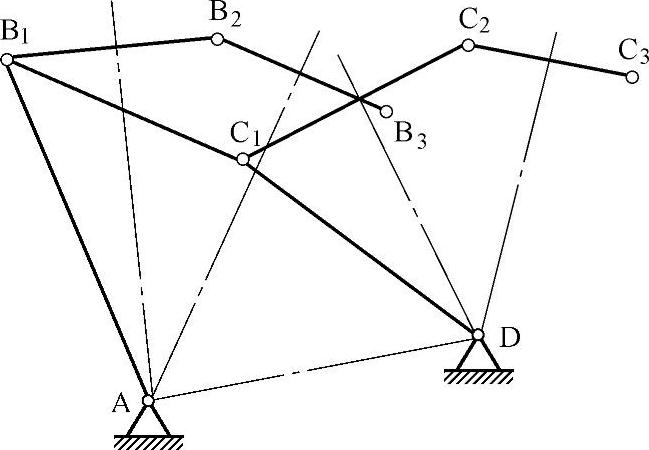
图3-92 按连杆位置设计

2）按照给定的行程速比系数K设计四杆机构，如图3-93、图3-94所示。

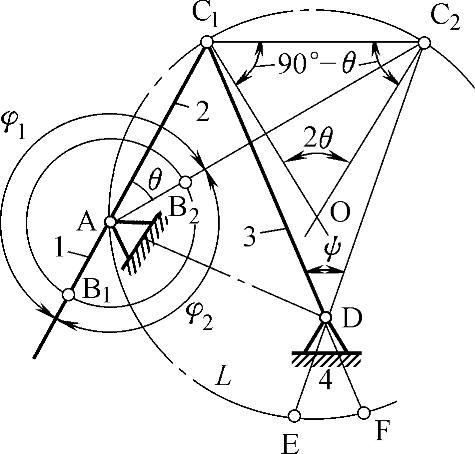
图3-93 按行程速比系数设计

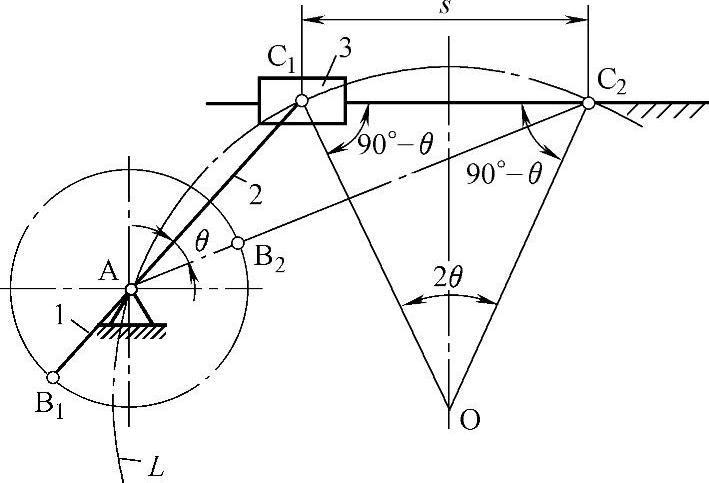
图3-94 按行程速比系数K设计曲柄滑块机构

3）按照给定的两连架杆位置设计四杆机构，如图3-95所示。

（2）解析法

按照给定两连架杆对应位置设计四杆机构。在图3-96所示的机构封闭多边形中，已知连架杆AB和CD的三对对应位置ϕ₁、ψ₁；ϕ₂、ψ₂和ϕ₃、ψ₃，要求确定各杆的长度l₁、l₂、l₃和l₄。此机构各杆长度按同一比例增减时，各杆转角间的关系不变，故只需确定各杆的相对长度。取l₁=1，则该机构的待求参数只有3个。

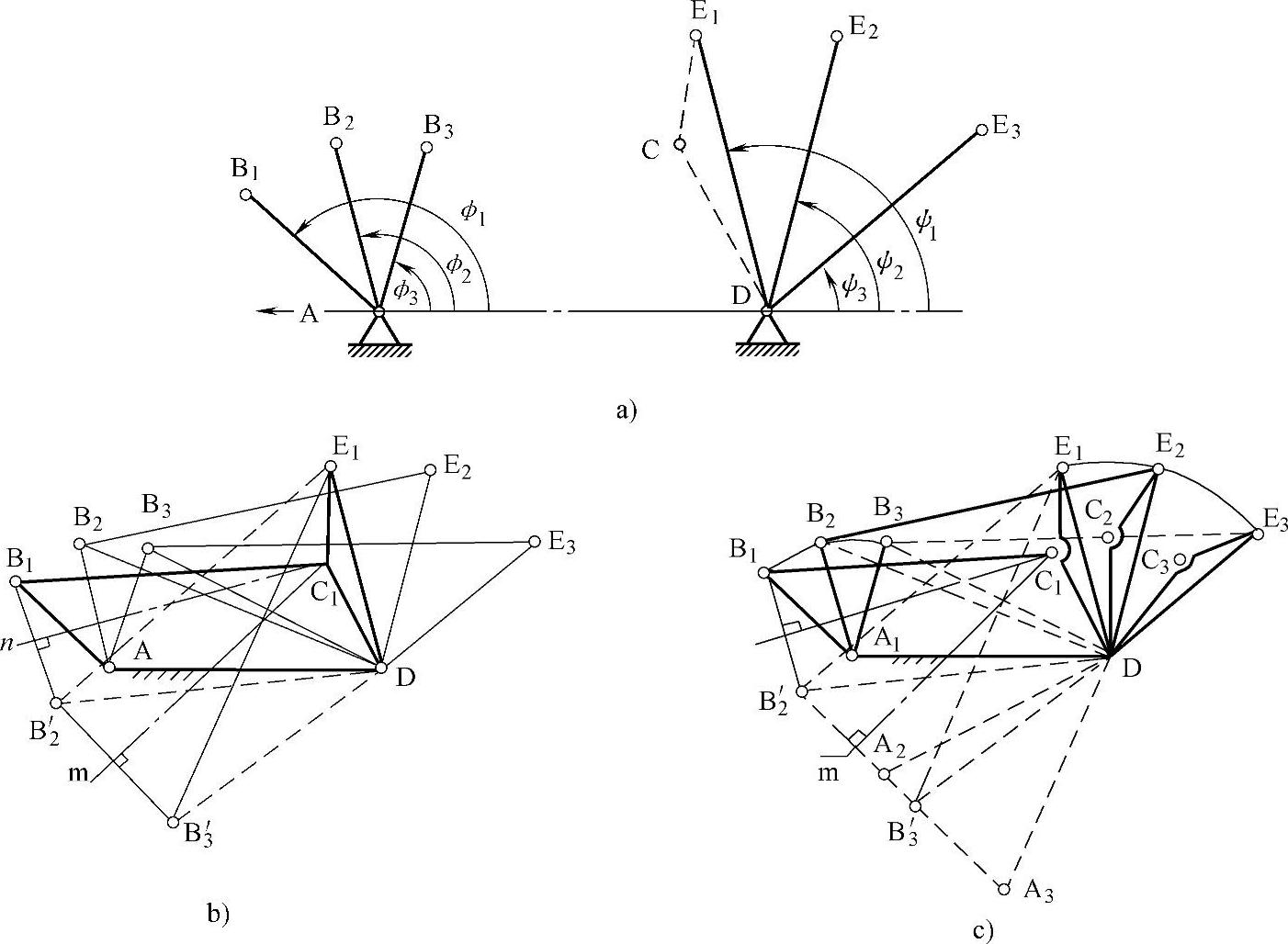
图3-95 按给定两连架杆位置设计四杆机构

该机构的4个杆组成封闭多边形。取各杆在坐标轴x和y上的投影，可以得到以下关系式：

cosϕ+l₂cosδ=l₄+l₃cosψ

sinϕ+l₂sinδ=l₃sinψ

将cosϕ和sinϕ移到等式右边，再把等式两边平方相加，即可消去δ，整理后得

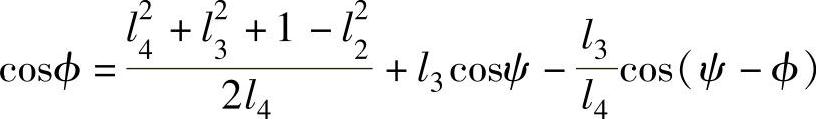
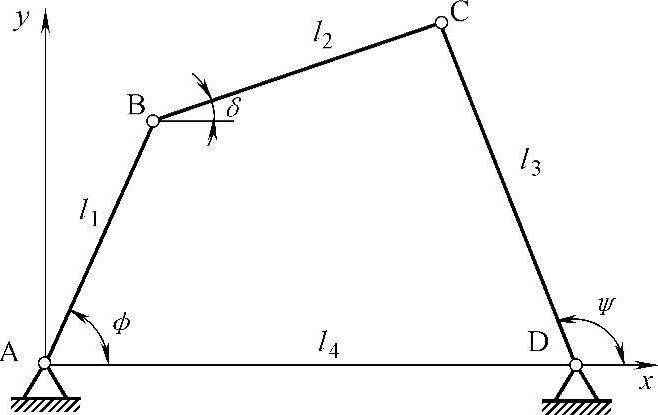
图3-96 机构封闭多边形

为简化上式，令

P₀=l₃

P₁=l₃/l₄

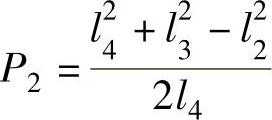
则有

cosϕ=p₀cosψ+p₁cos（ψ-ϕ）+p₂

上式即为两连架杆转角之间的关系式。将已知的三对对应转角ϕ₁、ψ₁，ϕ₂、ψ₂和ϕ₃、ψ₃分别代入上式中，可得到方程组

cosϕ₁=p₀cosψ₁+p₁cos（ψ₁-ϕ₁）+p₂

cosϕ₂=p₀cosψ₂+p₁cos（ψ₂-ϕ₂）+p₂

cosϕ₃=p₀cosψ₃+p₁cos（ψ₃-ϕ₃）+p₂

解出3个未知数p₀、p₁、p₂。将它们代入P₂=（l₄²+l²₃-l²₂）/2l₄，即可得l₂、l₃、l₄。以上求出的杆长l₁、l₂、l₃、l₄可同时乘以任意比例常数，所得的机构都能实现对应的转角。

（3）实验法

若给定连架杆的位置超过三对，也可以用实验法试凑，如图3-97所示。只能设计近似实现这一要求的四杆机构。下面举例说明。

实验法设计近似要求的四杆机构如图3-98所示。

①如图3-98a所示，在图纸上选取一点作为连架杆1的转动中心A，并任选AB₁作为连架杆1的l₁，根据给定的ψ₁₂、ψ₂₃、ψ₃₄和ψ₄₅做出AB₂、AB₃、AB₄和AB₅。

②选取连杆2的适当长度l₂，以B₁、B₂、B₃、B₄和B₅各点为圆心，l₂为半径，作圆弧K₁、K₂、K₃、K₄和K₅。

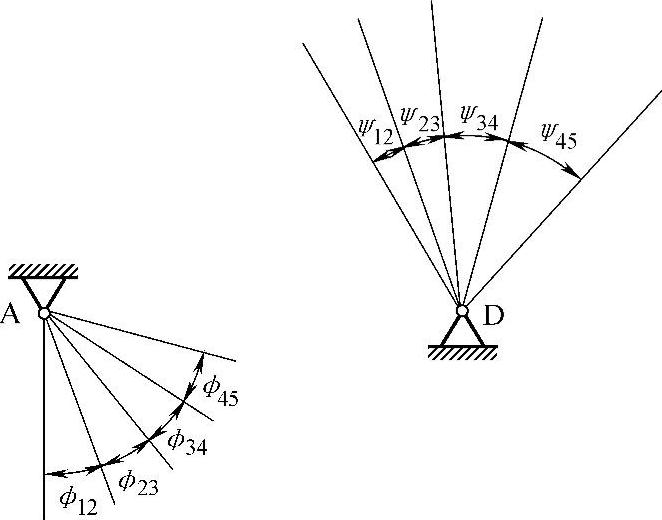
图3-97 给定连杆架杆四对位置

③另如图3-98b所示，在透明纸上选取一点作为连架杆3的转动中心D，并任选Dd₁作为连架杆3的第一位置，根据给定的ψ₁₂、ψ₂₃、ψ₃₄和ψ₄₅作出Dd₂、Dd₃、Dd₄和Dd₅。再以D为圆心，用连架杆3可能的不同长度为半径作许多同心圆弧。

将画在透明纸上的图3-98b覆盖在图3-98a上（见图3-98c）进行试凑。使圆弧K₁、K₂、K₃、K₄、K₅分别与连架杆3的对应位置Dd₁、Dd₂、Dd₃、Dd₄和Dd₅的交点C₁、C₂、C₃、C₄、C₅均落在以D为圆心的同一圆弧上，则图形AB₁C₁D即为所要求的四杆机构。如果移动透明纸，不能使交点C₁、C₂、C₃、C₄、C₅落在同一圆弧上，那就需要改变连杆2的长度，然后重复以上步骤，直到这些交点正好落在或近似落在透明纸的同一圆弧上为止。

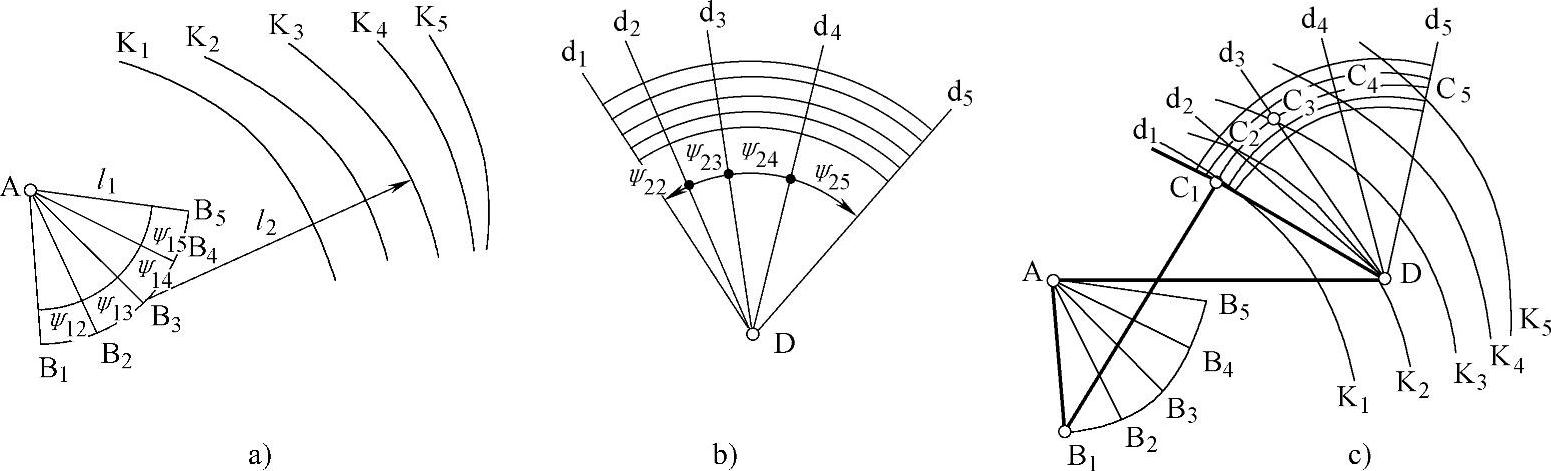
图3-98 实验法设计近似要求的四杆机构

5.平面机构的运动分析及传动分析

机构运动分析的目的：

1）在设计新的机械或分析现有机械的工作性能时，要计算其机构的运动参数。

2）为了确定某一构件的行程，或确定机壳的轮廓，或避免构件之间碰撞干涉等，要确定机构某些点的运动轨迹。

3）为了确定机械的工作条件，要确定其机构构件上某些点的速度。

4）为了确定惯性力，要进行机构的加速度分析。

机构运动分析的方法同平面四杆机构的设计方法一样，有图解法、解析法和实验法三种。

（1）速度瞬心法及其在机构速度分析上的应用

当两个构件相对运动时，两构件上相对速度为零的重合点或瞬时绝对速度相同的重合点称为瞬心。速度瞬心有相对速度瞬心（两构件都是运动的）和绝对速度瞬心（两构件之一是静止的）。速度瞬心用符号P₁₂表示，如图3-99所示。

1）机构中瞬心的数目：在机构中的瞬心数目遵循组合规律，任意两构件之间具有一个瞬心。

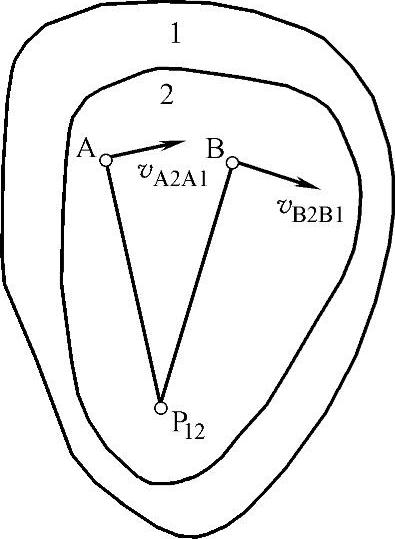
图3-99 速度瞬心表示

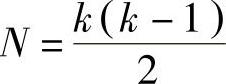
式中 N——机构中的瞬心数目；

k——构件数目。

2）瞬心位置的确定：

已知两构件的相对运动或形成运动副的两构件时，根据瞬心定义直接求两构件的瞬心。

①当两构件用转动副连接时，瞬心位于转动副中心，如图3-100所示。

②当两构件组成移动副时，瞬心位于导路的垂直方向的无穷远处，如图3-101所示。

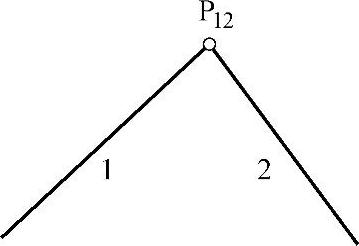
图3-100 两构件用转动副连接时的瞬心

图3-101 两构件组成移动副时的瞬心

③当两构件组成纯滚动的高副时，瞬心位于接触点，如图3-102所示。

④当两构件组成滑动兼滚动的高副时，瞬心位于过接触点的公法线n-n上，如图3-103所示。

不形成运动副的两构件，根据三心定理求两构件的瞬心。

三心定理：做平面平行运动的3个构件共有3个瞬心，它们位于同一直线上，如图3-104所示。

例：求图3-105所示的铰链四杆机构所有的速度瞬心。

图3-102 两构件组成纯滚动的高副连接时的瞬心

图3-103 两构件组成滑动兼滚动的高副连接时的瞬心

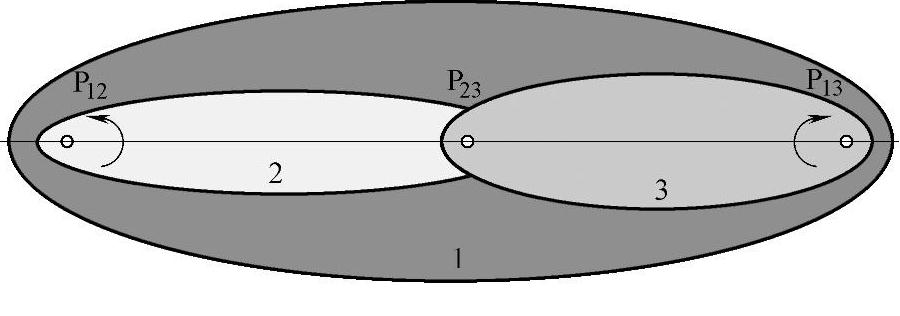
图3-104 不形成运动副的两构件的瞬心（三心定理）

解：a.计算瞬心数目

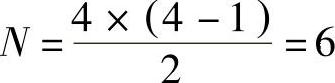
b.根据瞬心定义求解。该机构的转动副A、B、C及D分别为瞬心P₁₄、P₁₂、P₂₃及P₃₄。

c.构件1与3的瞬心，构件2与4的瞬心求法如图3-106所示。

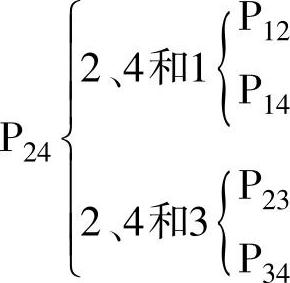
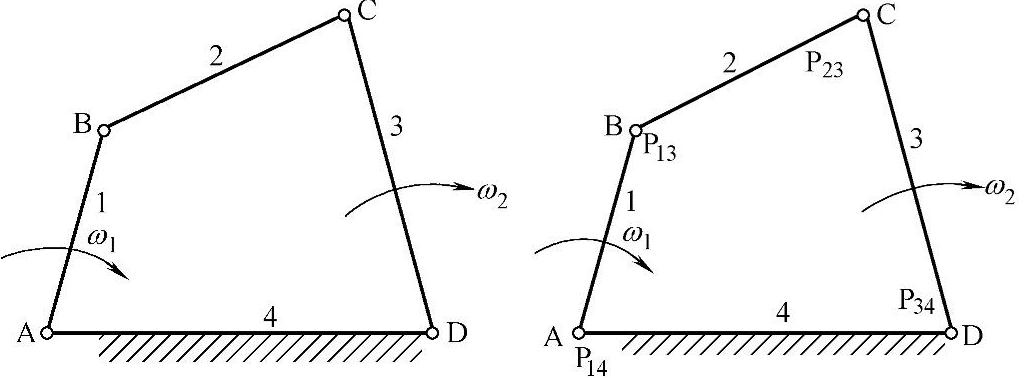
图3-105 铰链四杆机构

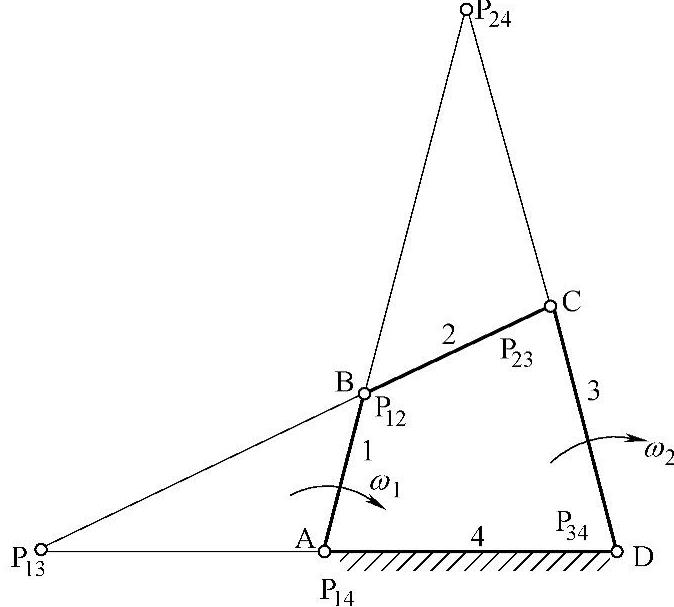
图3-106 不形成运动副的两构件的瞬心求法

d.结果：铰链四杆机构的6个瞬心，如图3-107所示。

3）速度瞬心法在机构速度分析上的应用：速度瞬心法在机构构件数目较少时用，且只能对机构进行速度分析，不能对加速度进行分析。

a.铰链四杆机构

原动件1与从动件3的瞬时角速度之比。

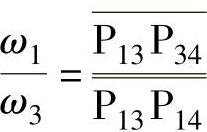
b.曲柄滑块机构

已知构件1的角速度ω₁，求滑块C的速度。

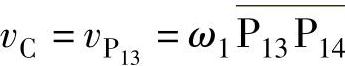
c.滑动兼滚动接触的高副机构

原动件2与从动件3的瞬时角速度之比。

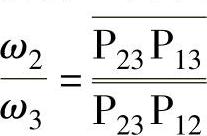
结论：组成滑动兼滚动高副的两构件，其角速度与连心线被轮廓接触点公法线所分割的两线段长度成反比。

d.滑动兼滚动接触的高副机构

原动件1与从动件2（移动）的速度关系。

（2）相对运动图解法

用相对运动原理列出构件上点与点之间的相对运动矢量方程，然后作图求解矢量方程，适于求机构的速度和加速度。相对运动（又称平面运动合成）原理可分为基点法和重合点法两种。

基点法：刚体（构件）的平面运动分解为随基点的平动加上绕基点的转动，用于求在同一构件上的点间的速度和加速度的关系。

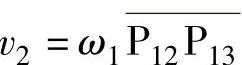
重合点法（点的速度合成定理）：动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速度的矢量和。

■组成移动副两构件的重合点间的速度和加速度的关系

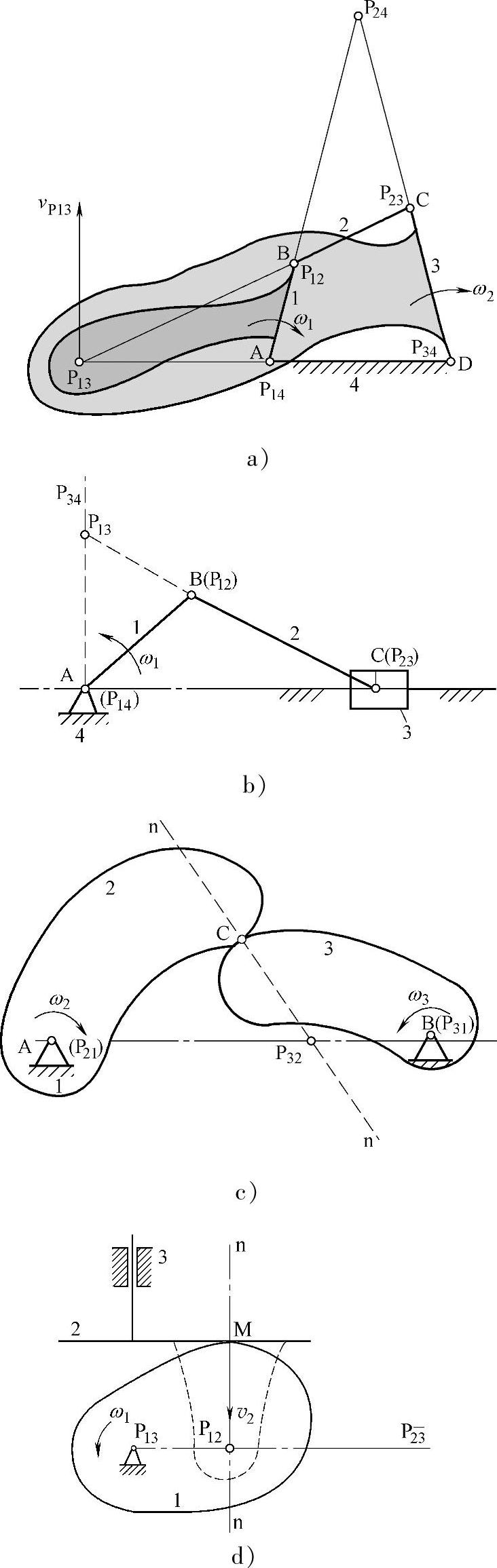
图3-107 铰链四杆机构的6个瞬心

1）在同一构件上的点间的速度和加速度的求法（基点法）：图3-108所示的铰链四杆机构中，已知各构件的长度及构件1的位置、角速度ω₁和角加速度α₁，求构件2的角速度ω₂、角加速度α₂及其上点C的速度^→_vc和加速度_a^→_c、点E的速度^→_vE和加速度_a^→_E，以及构件3的角速度ω₃和角加速度α₃。在任意两点B、X之间

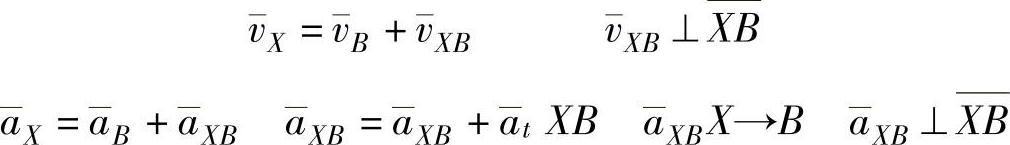
构件绕基点O的定轴转动

(www.xing528.com)

构件随基点的平动（沿导轨滑动）

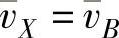
2）速度影像（梅姆克第一定理）定理：一个刚体上3个点的速度矢量末端在速度平面图中所构成的三角形与原始三角形同向相似，且沿刚体的角速度方向转过90°，如图3-109所示。

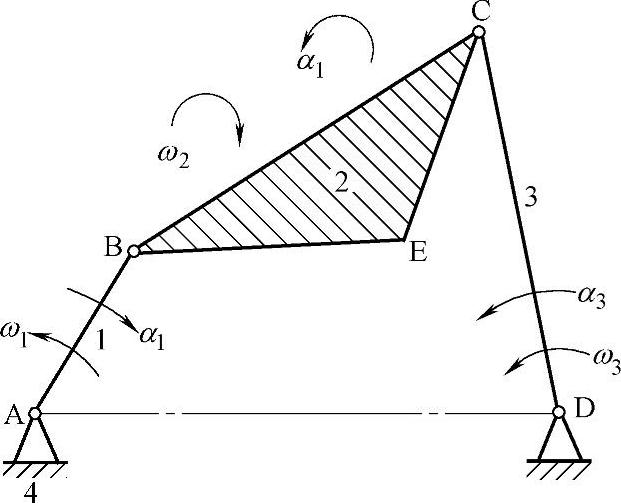
图3-108 铰链四杆机构

①p称为极点，代表所有构件上绝对速度为零的点。

②运动简图中任意点的影像以同名小写字母表示。

连接点p与任一点的矢量便代表该点在机构图中的同名点的绝对速度，其指向是从p指向该点。如p→x代表v_X。

连接其他任意两点的矢量便代表该两点在机构图中的同名点间的相对速度，其指向与速度的角标相反。如x→y代表v_YX。

③速度影像的应用条件是同一构件内。

④构件绕基点O的定轴转动

⑤构件随基点的平动（沿导轨滑动）

3）加速度影像（梅姆克第二定理）定理：一个刚体上3个点的加速度矢量末端在加速度平面图中所构成的三角形与原始三角形同向相似，如图3-109所示。

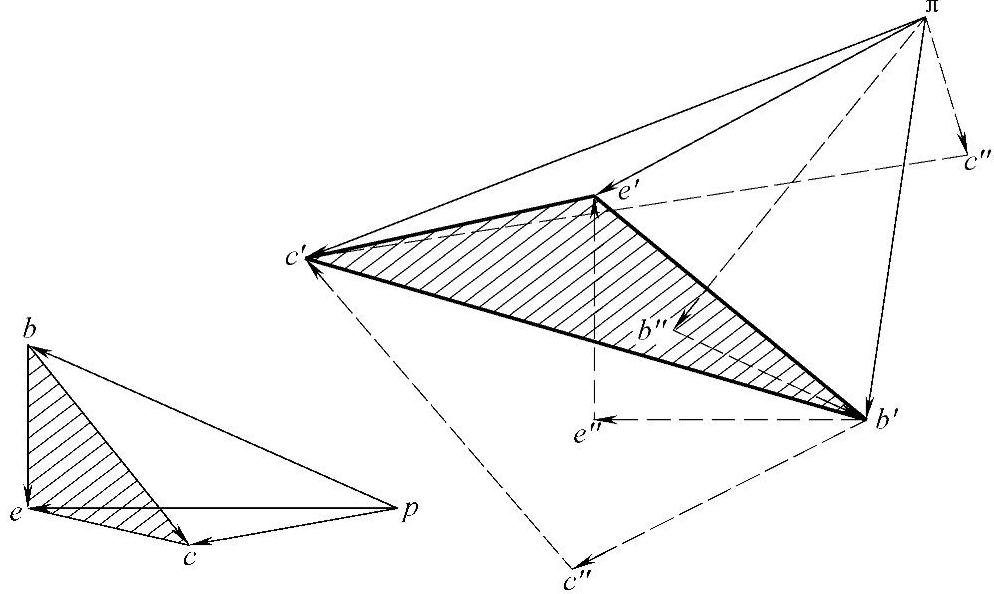
图3-109 速度影像及加速度影像（梅姆克第一及第二定理）定理

①π称为极点，代表所有构件上绝对加速度为零的点。

②连接点π与任一点的矢量便代表该点在机构图中的同名点的绝对加速度，其指向是从π指向该点。如π→x′代表示a_X。

③连接带有角标′的其他任意两点的矢量便代表该两点在机构图中的同名点间的相对加速度，其指向与加速度的角标相反。如x′→y′代表a_YX。

④加速度分量一般用虚线表示。切向加速度用同名而不同上标的两个字母表示，方向指向单撇（′）点。如y″→y′代表a^t_YX，而Y→X的向心加速度x′→y″代表aⁿ_YX。

4）组成移动副两构件的重合点间的速度和加速度的求法（重合点法）：图3-110a所示的四杆机构中，已知机构的位置、各构件的长度及构件1的等角速度ω₁，求构件3的角速度ω₃和角加速度α₃。

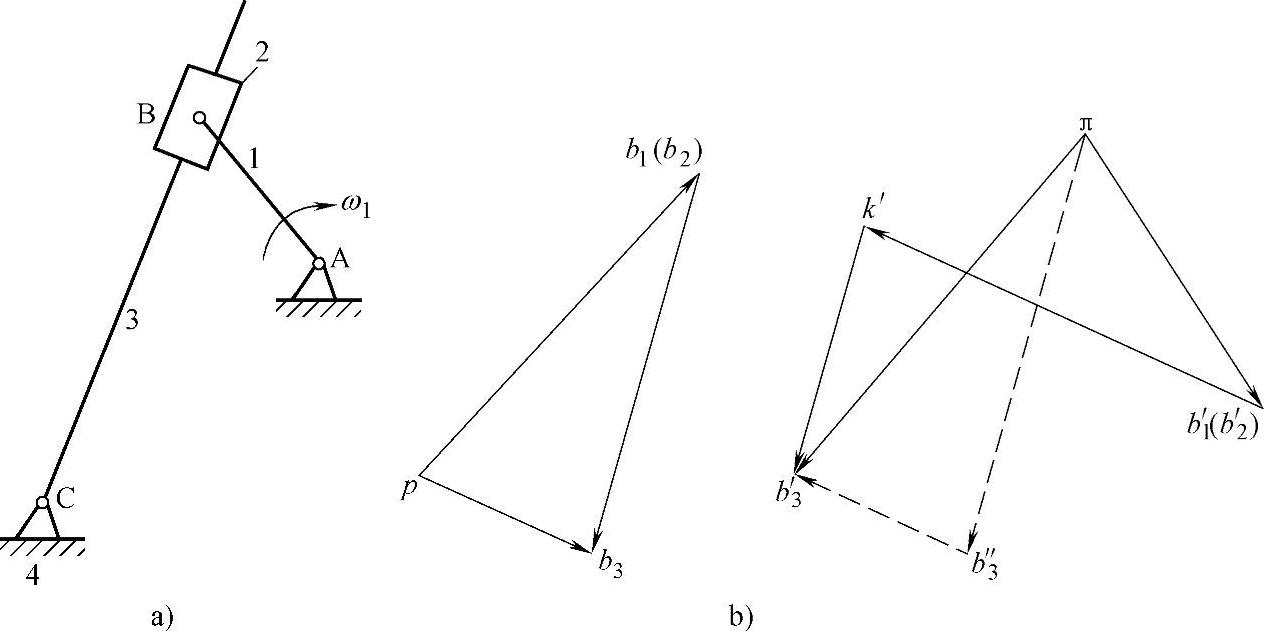
图3-110 用重合点法求四杆机构的速度和加速度

解：构件2与3组成移动副，构件2上点b₂与构件3上点b′₃是重合点，如图3-110b所示。

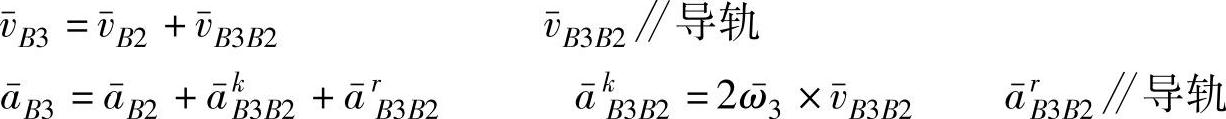
（3）用解析法求机构的速度和加速度

◆如何从图解法迁移到解析法

■矢量法：

•位置（位移）分析需要求解非线性方程组

◆二级机构消元求根的可能性

◆三级及以上机构数值求解方法

•速度及加速度分析仅求解线性方程组

矢量的复数表示法：a_y

复数矢量法是将机构看成一封闭矢量多边形，并用复数形式表示该机构的封闭矢量方程式，再将矢量方程式分别对所建立的直角坐标系取投影。

1）用解析法求铰链四杆机构的速度和加速度：在图3-111a所示的铰链四杆机构中，已知杆长分别为l₁、l₂、l₃、l₄，原动件1的转角为φ₁及等角速度为ω₁，要求确定构件2、3的角位移φ₂、φ₃，角速度ω₂、ω₃和角加速度ε₂、ε₃。

解：①位置分析，建立坐标系

封闭矢量方程式：

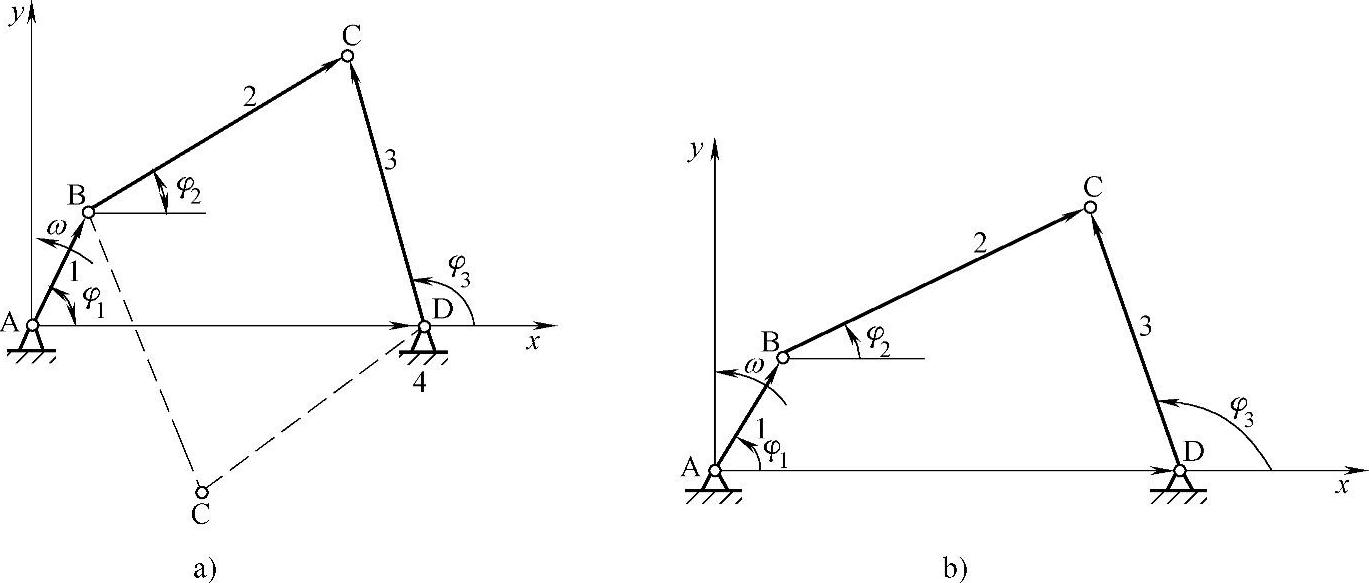
图3-111 用解析法求铰链四杆机构的速度和加速度

封闭矢量方程式分解，以复数形式表示：

l₁e^iφ1+l₂e^iφ2=l₄+l₃e^iφ3欧拉展开：l₁（cosφ₁+isinφ₁）+l₂（cosφ₂+isinφ₂）=l₄+l₃（cosφ₃+isinφ₃）

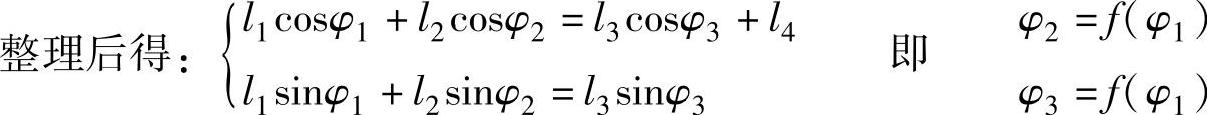
解方程组得

Acosφ₃+Bsinφ₃+C=0

A=l₄-l₁cosφ₁

B=-l₁sinφ₁

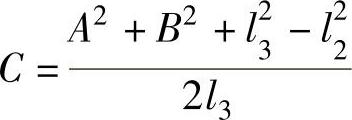
换元，求根

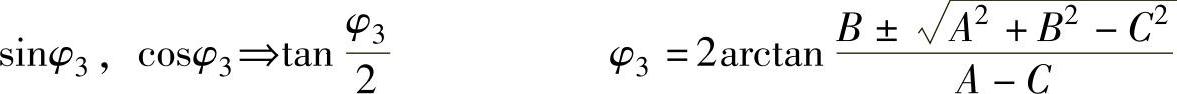
回代

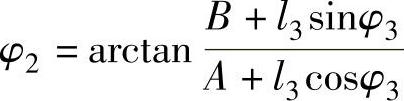
②速度分析：将封闭矢量方程式对时间t求导得

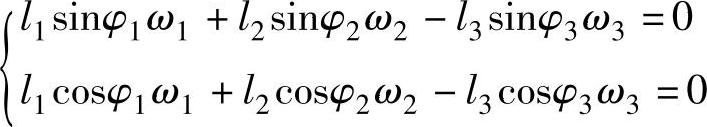
l₁iω₁e^iφ1+l₂iω₂e^iφ2=l₃iω₃e^iφ3

可用克莱姆法则求解

消去ω₂，两边乘e^-iφ2得

l₁ω₁ie^{i（φ1-φ2）}+l₂ω₂ie^{i（φ2-φ2）}=l₃ω₃ie^{i（φ3-φ2）}

按欧拉公式展开，取实部相等，得

同理求得

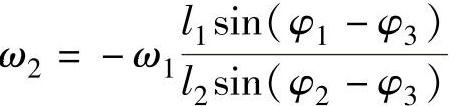
角速度为正表示逆时针方向，角速度为负表示顺时针方向。

③加速度分析：用l₁iω₁e^iφ1+l₂iω₂e^iφ2=l₃iω₃e^iφ3对时间求导或用封闭矢量方程式对时间t二次求导得

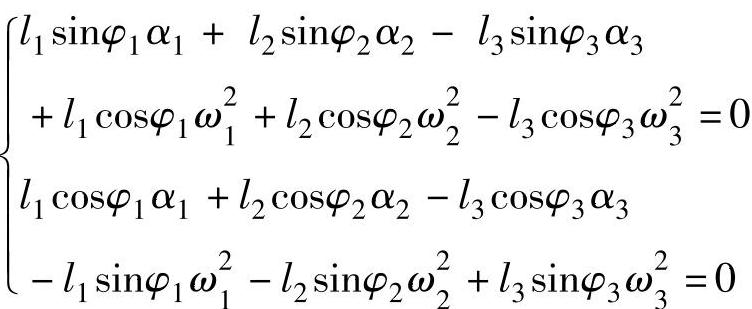
可用克莱姆法则求解。

2）本节小结：

①位置方程组是非线性，速度、加速度方程组是线性，且特征矩阵相同。

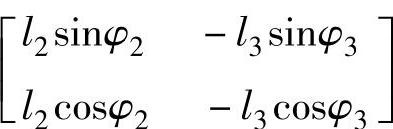
②牛顿-拉普森法泰勒多项式

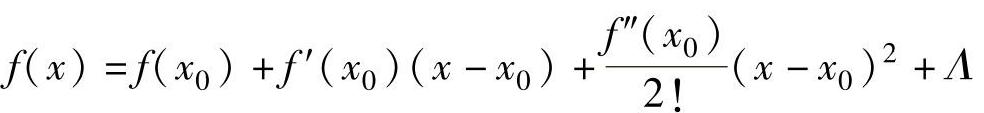
♦设ζ是非线性方程f（x）=0的一个解，则f（ζ）=0。

♦由泰勒公式对于任何x有f（ζ）=f（x）+f′（x）（ζ-x）+…。

♦取前两项得方程0=f（x）+f′（x）Δx（1），此时Δx≈ζ-x，即ζ≈x+Δx。

♦将一确定数值赋给x，那么x的修正值Δx可以由线性方程（1）求得。在收敛的情况下，x+Δx比x更接近ζ。反复将修正结果代入方程（1）求解，再修正，可得到足够精度的ζ数值解。

♦对于方程组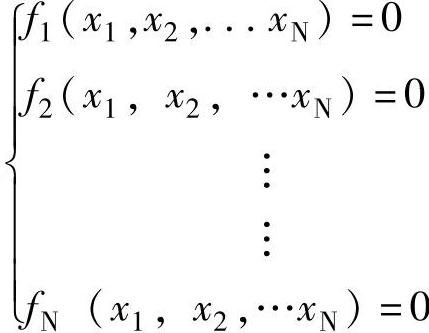可构造出线性方程组。

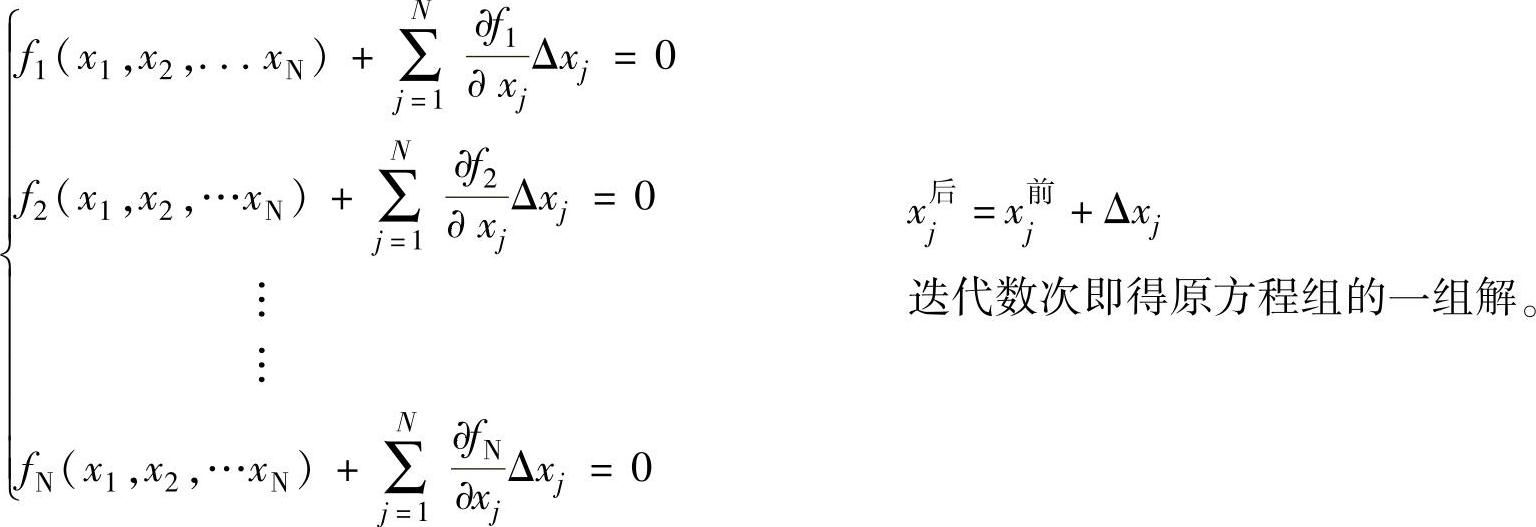
③封闭（环路）矢量方程：

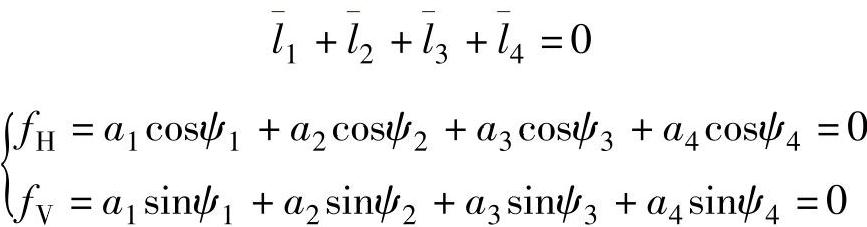
（ψ₂，ψ₃）待求，设近似解为（ϕ₁，ϕ₂），令q=ψ₁，则剩余函数为

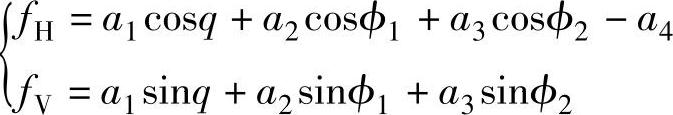
所构造方程组右侧值即为相伴的雅可比矩阵为（左侧系数）

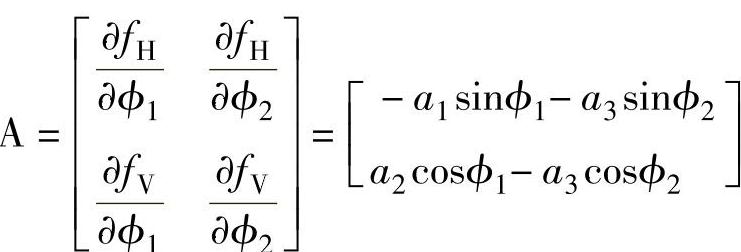
一般算法形式（第i次迭代）

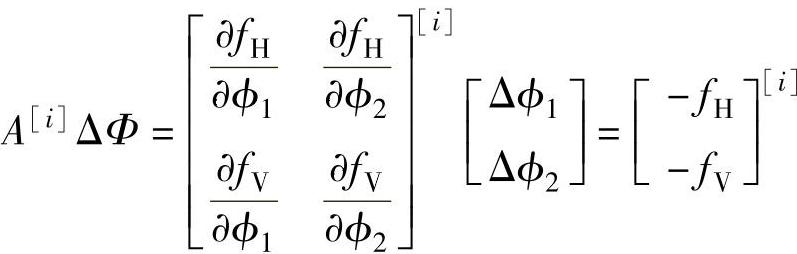
第i+1个修正结果

④注意事项：

ⅰ初值的获得，可由量角器测出（常无精度要求），单位为rad；

ⅱ某些位置可能不收敛；

ⅲ为节省计算量，达到一定精度即可停止迭代。

3）运动线图：运动量用线图表示，能迅速了解其时间上或局部的变化概貌。

运动线图的主要表示形式有：

①位移-时间线图（s-t线图）；

②速度-时间线图（v-t线图）；

③加速度-时间线图（a-t线图）；

④速度-位移线图（v-s线图）。

（4）凸轮机构及其设计

在断路器操动机构中，凸轮和微动开关（带滚子从动件、弹簧力锁合）结合组成凸轮机构常用来控制储能位置或压力，这些场合的承载能力不高又要求从动件的位移必须严格按照精确的预定规律变化，常用的有盘形转动和直线移动凸轮机构，为平面凸轮机构。图3-120a所示为某种机构的凸轮压力开关。

1）凸轮机构的组成及从动件的运动轨迹：凸轮机构通常由凸轮（具有曲线轮廓或凹槽的构件，通过高副接触）和从动件（平动、转动）、机架组成。

尖底偏置直动从动件盘形凸轮机构如图3-112a所示，其凸轮轮廓上最小矢径为半径的圆称为基圆，直动从动件的中心至凸轮的转动圆心称为偏心距e。

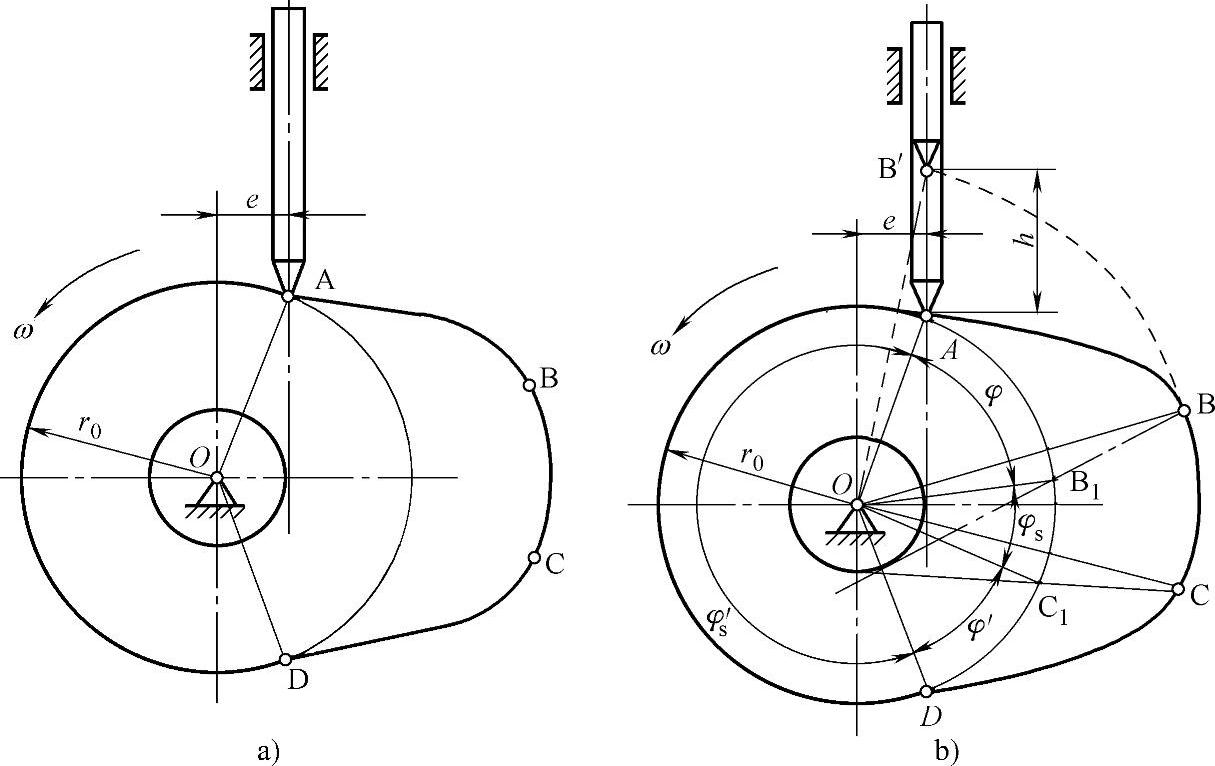
图3-112 尖底偏置直动从动件盘形凸轮机构

直动从动件的运动轨迹如图3-112b所示，从动件的最大位移称为行程h。除此之外还有下列几何关系：

推程运动角：φ=BOB′=∠AOB₁

远休止角：φ_s=∠BOC=∠B₁OC₁

回程运动角：φ′=∠C₁OD

近休止角：φ_s′=∠AOD

此从动件的运动轨迹规律为上升停降停，如图3-113所示。

2）常用从动件的运动规律分析：

a.匀速运动规律（推程段）

在这个阶段从动件由于加速度发生无穷大突变而引起的冲击称为刚性冲击，如图3-114所示。

图3-113 从动件的运动轨迹规律

b.等加速等减速运动规律（推程及回程段）

在这个阶段，从动件由于加速度发生有限值的突变称为柔性冲击，如图3-115所示。这种运动规律适用于中速场合。

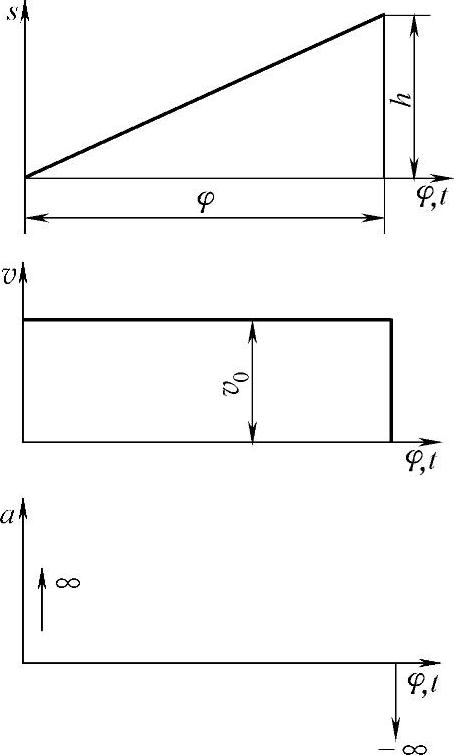
图3-114 匀速运动规律（推程段）的刚性冲击

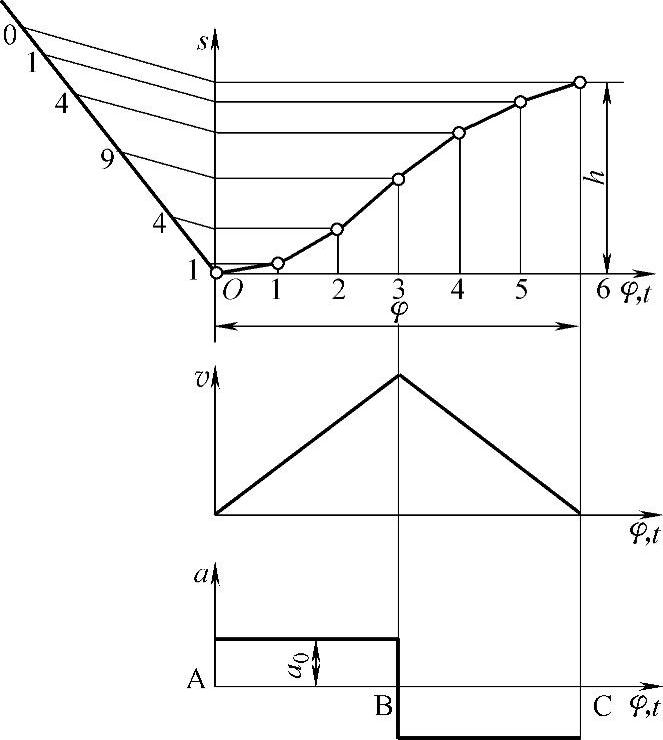
图3-115 等加速等减速运动规律的柔性冲击

c.加速度按余（正）弦运动规律变化（行程段）

如图3-116a、b所示，余弦运动在这个阶段从动件的加速度有如下运动特征：

若φ_s，φ_s′为零，无冲击；

若φ_s，φ_s′不为零，有冲击。

正弦运动在这个阶段从动件加速度的运动特征没有冲击，如图3-116b所示。

d.组合运动规律

为了获得更好的运动特征，可以把上述几种运动规律组合起来应用，组合时，两条曲线在拼接处必须保持连续。

3）用反转作图法设计直动从动件盘形凸轮机构的凸轮轮廓。

反转作图法设计凸轮轮廓如图3-117所示。

a.尖底直动从动件盘形凸轮机构凸轮轮廓设计

已知γ₀，e，S-φ，ω和转向，用作图法作图如图3-118所示。

图3-116 从动件加速度按余弦运动规律变化

a）余弦运动从动件的运动特征 b）正弦运动从动件的运动特征

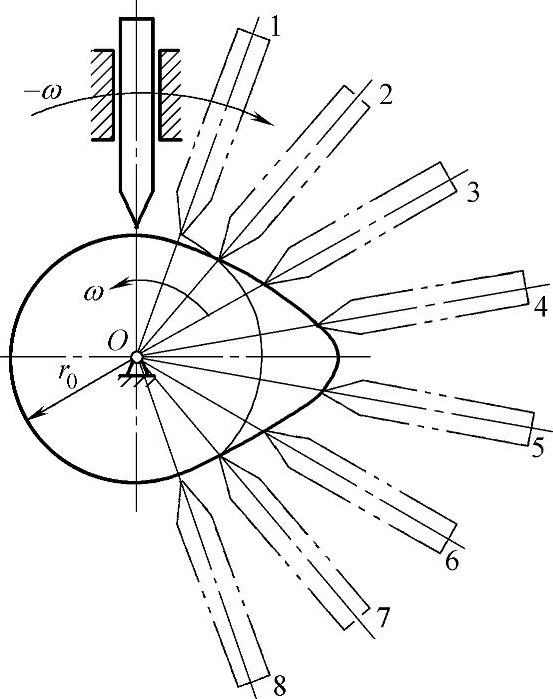
图3-117 反转作图法设计凸轮轮廓

b.滚子直动从动件

已知γ₀，e，S-φ，ω和转向，用作图法作图如图3-119所示。步骤如下：

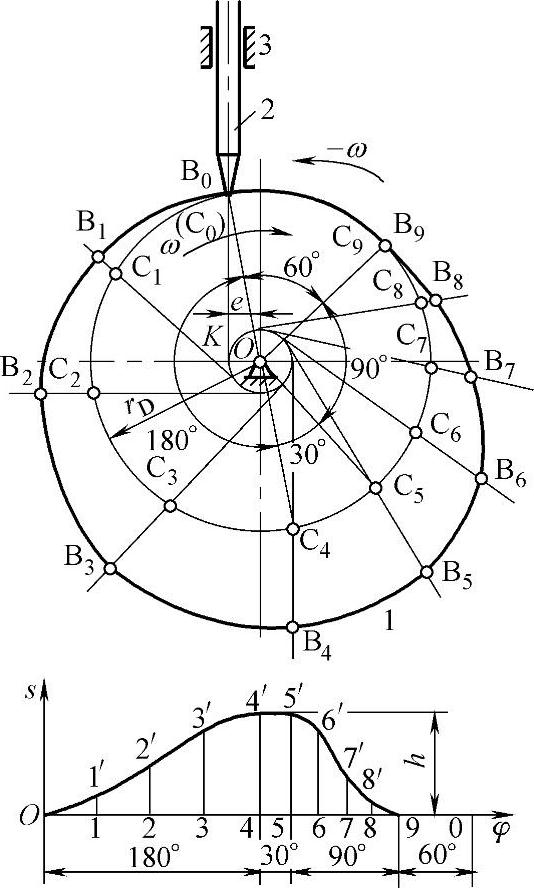
图3-118 尖底直动从动件盘形凸轮轮廓设计

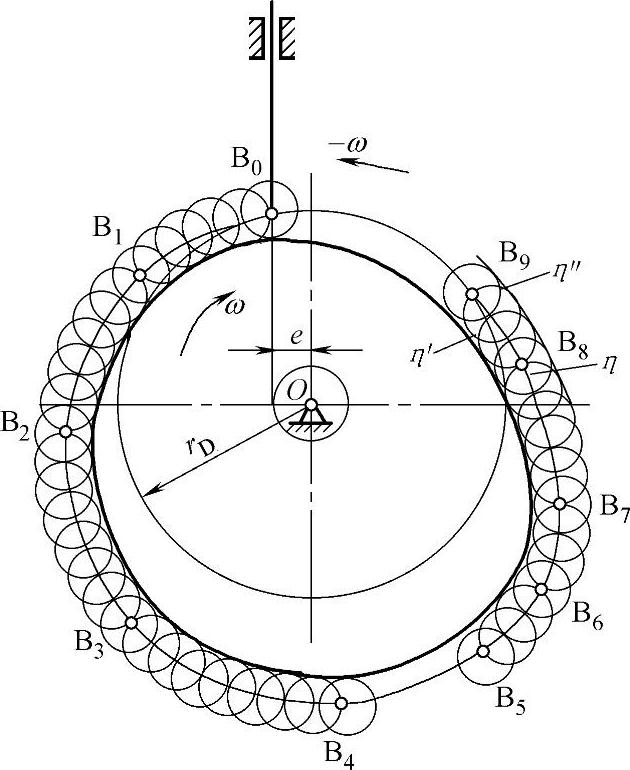
图3-119 滚子直动从动件盘形凸轮轮廓设计

①去掉滚子，以滚子中心为尖底；

②按照上述方法作出轮廓曲线——理论轮廓曲线；

③在理论轮廓上画出一系列滚子，画出滚子的内包络线——实际轮廓曲线。

注意：设计滚子从动件凸轮机构时，凸轮的基圆半径是指理论轮廓曲线的基圆半径。

c.摆动从动件盘形凸轮机构凸轮轮廓设计

已知：ω转向，r₀，a，l，ψ_max，ϕ-ψ，用作图法作图如图3-120b所示。

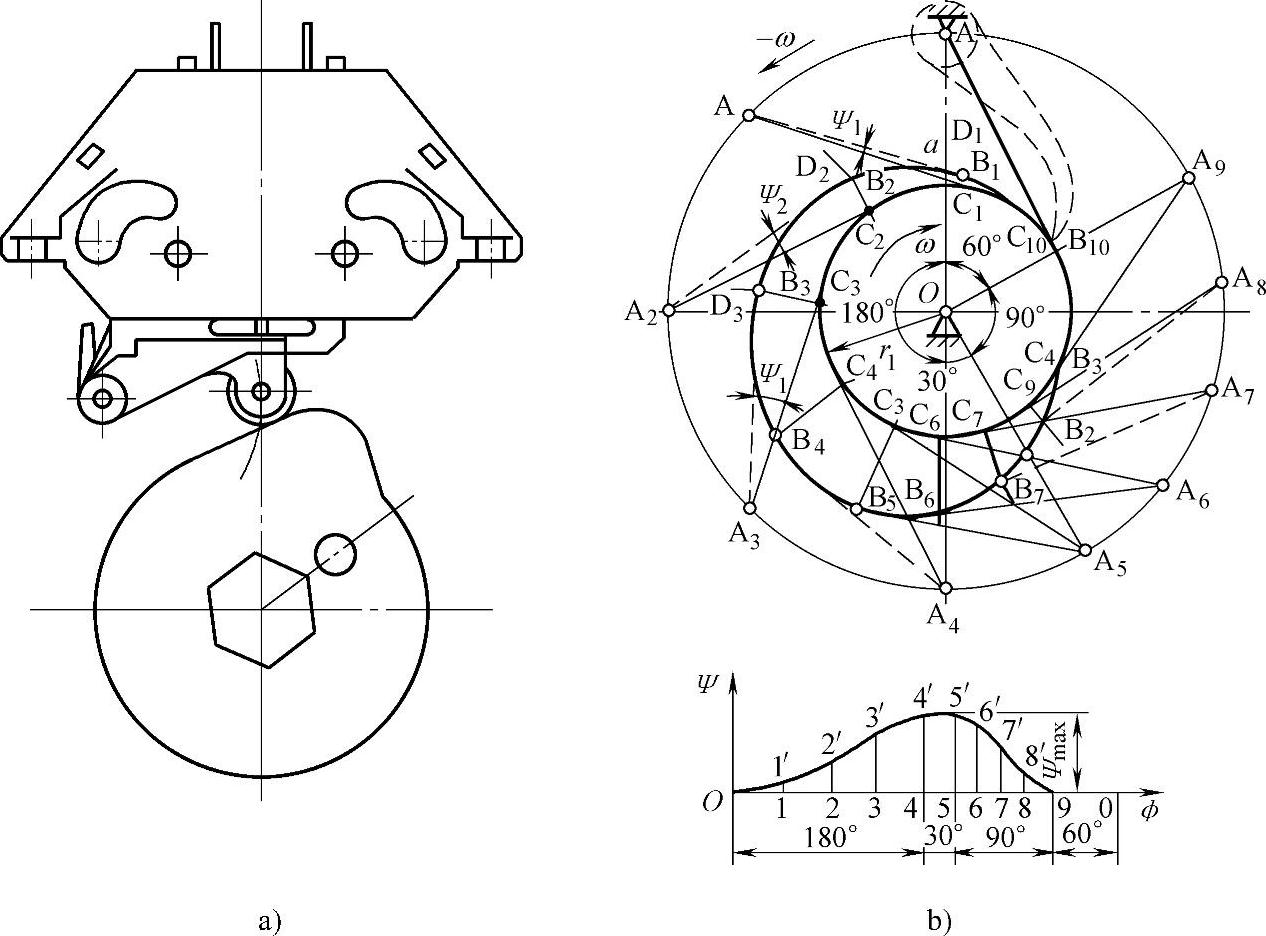
图3-120 摆动从动件盘形凸轮轮廓设计

a）凸轮压力开关 b）摆动从动件凸轮轮廓设计

4）用解析法设计凸轮机构的凸轮轮廓曲线：

滚子从动件盘形凸轮

a.理论轮廓曲线方程：

①直动从动件盘形凸轮机构

图3-121所示的偏置直动滚子从动件盘形凸轮机构轮廓线。求凸轮轮廓线的方程，反转法给整个机构一个绕凸轮轴心O的公共角速度-ω，这时凸轮将固定不动，而从动件将沿-ω方向转过角度φ，滚子中心将位于B点。B点的坐标，亦即理论轮廓线的方程为

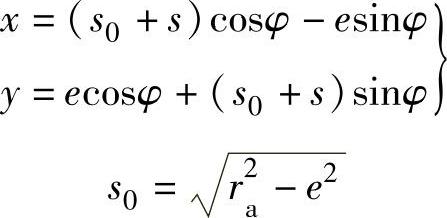
式中 r_a——理论轮廓线的基圆半径。

对于同心从动件凸轮机构，因e=0，所以s₀=r_a

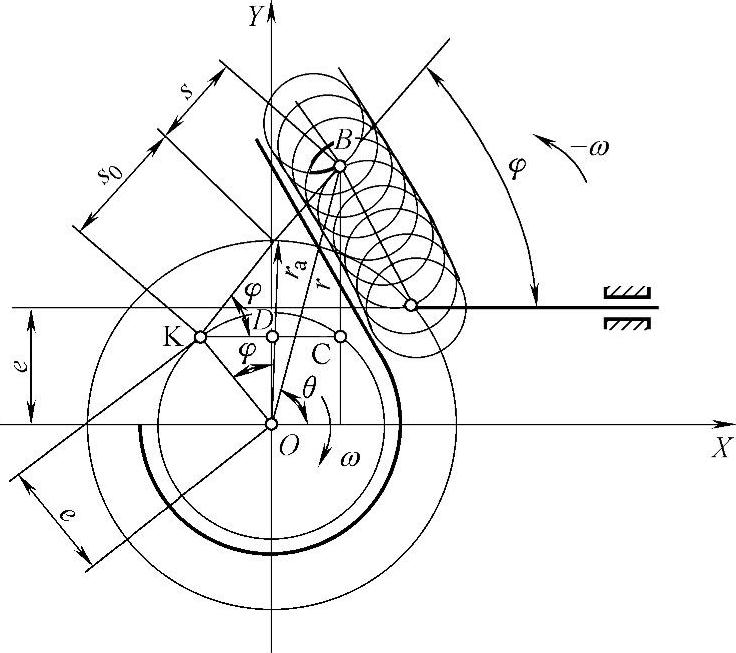
图3-121 解析法设计偏置直动滚子从动件盘形凸轮机构轮廓线

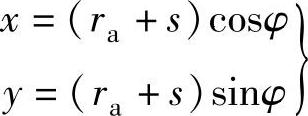
②摆动从动件盘形凸轮机构

摆动滚子从动件盘形凸轮机构，仍用反转法使凸轮固定不动，而从动件沿-ω方向转过角度，滚子中心将位于B点。B点的坐标，亦即理论轮廓线的方程为

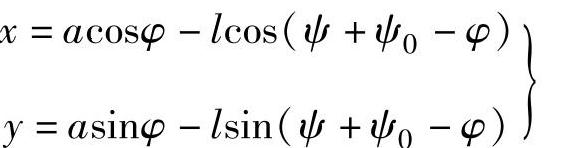
ψ₀为从动件的起始位置与轴心连线OA₀之间的夹角。

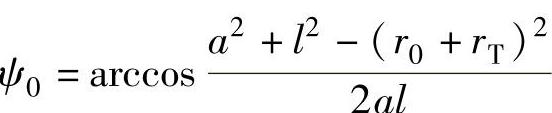
在设计凸轮轮廓线时，通常e、r₀、r_T、a、l等是已知的尺寸，而s和ψ是φ的函数，它们分别由已选定的位移方程s=s（ψ）和角位移方程ψ=ψ（ψ）确定。

b.实际轮廓线方程

滚子从动件盘形凸轮的实际轮廓线是圆心在理论轮廓线上的一族滚子圆的包络线。由微分几何可知，包络线的方程为

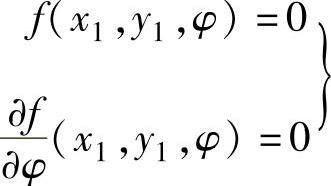
式中 x₁、y₁——凸轮实际轮廓线上点的直角坐标。

对于滚子从动件凸轮，由于产生包络线（即实际轮廓线）的曲线族是一族滚子圆，其圆心在理论轮廓线上，所以由上式有：

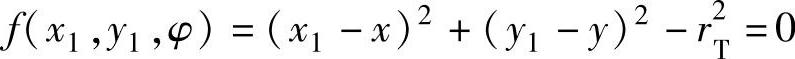
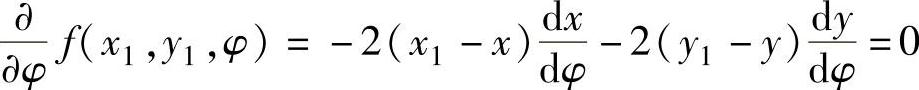
联立求解x₁和y₁，得滚子从动件盘形凸轮的实际轮廓线参数方程：

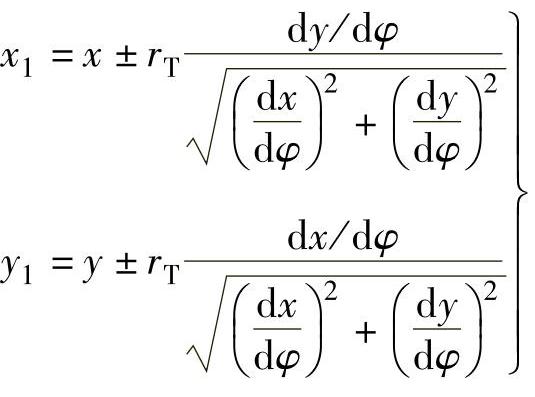
上面的一组加减号表示一根外包络廓线，下面的一组加减号表示另一根内包络廓线。

5）凸轮机构基本尺寸的确定：

a.凸轮机构的压力角和自锁

接触点法线与从动件上作用点速度方向所夹的锐角称为压力角，如图3-122所示。

b.自锁

极限压力角α_lim→l₂，l₁，f，润滑

摆动从动件：[α]=40°～50°

直动从动件：[α]=30°～38°

c.按许用压力角确定凸轮回转中心位置和基圆半径

滚子（尖底）直动从动件盘形凸轮机构

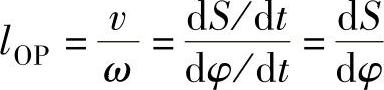
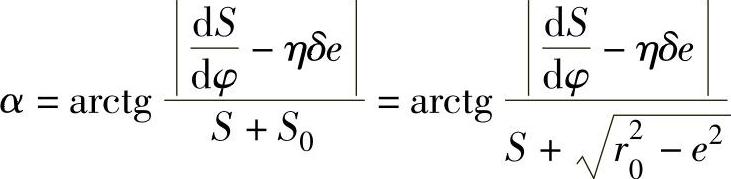
式中 η——转向系数；

δ——从动件偏置方向系数。

由式可知：r₀↓α↑

d.滚子半径的选择

滚子半径r_T必须小于理论轮廓曲线外凸部分的最小曲率半径ρ_min，设计时，r_T<0.8ρ_min，如图3-123所示。

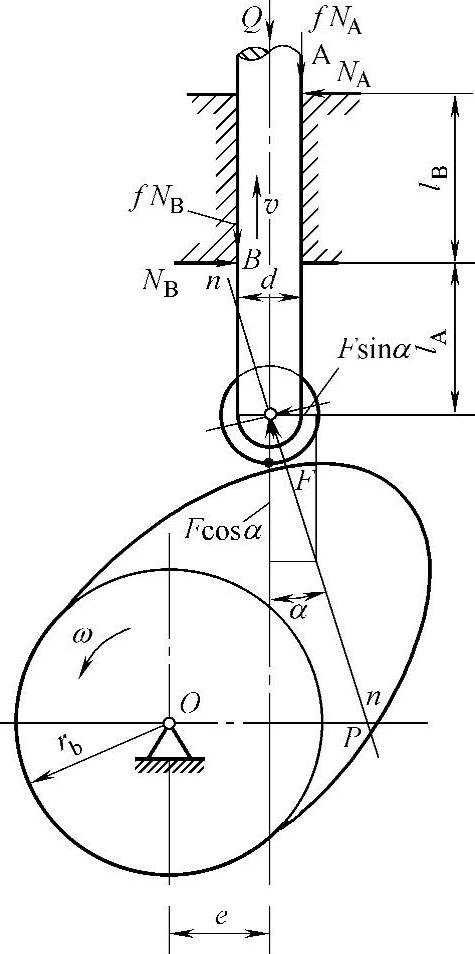
图3-122 凸轮机构的压力角和自锁

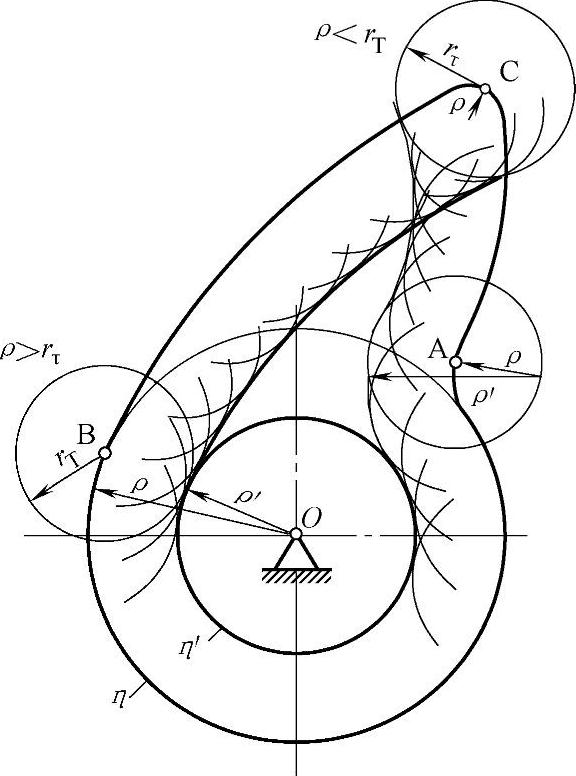
图3-123 从动件滚子半径的选择

（5）平面机构的传动分析

根据前面所述平面机构的运动分析，验算断路器的传动系统性能，确认是否达到要求。机构的传动特性实际上就是机构的输出功在各点位置上所输出的力矩特性，机构和断路器的特性配合关系有包容配合和相交配合，具体采用哪一种要根据机构的种类和传动原理来决定。相交配合只要相交点选择得当，机构不但能很好地完成预定动作，且机构能量得到充分的发挥利用，机械效率较高。预定动作完成后，剩余残能较小，冲击、振动减弱，可靠性提高。一般断路器产品中，气动机构和液压机构采用包容配合，弹簧机构采用相交配合。包容配合对外界阻力变化敏感度较低，相交配合则较高。

1）断路器分合闸速度计算要点：断路器的分、合闸速度，是指在分、合闸过程中断路器动触头的运动速度。其主要特性参数有分闸速度（刚分点）、最大分闸速度、平均分闸速度和分闸末尾速度（缓冲后到达运动终点前的速度）、合闸速度（刚合点）、平均合闸速度和合闸末尾速度（缓冲后到达运动终点前的速度）。它们是控制断路器开断、关合的重要技术参数。

利用能量守恒定理，可以计算出断路器动触头的运动速度，其步骤是：

①选择动触头为归算点，将运动系统中的各元件的质量等价地归算到动触头上，得到总的归算质量∑m_c；

②将作用在运动系统中的各种力等价地归算到动触头上，得到总归算力∑F_c。一般∑F_c为触头行程l的函数，如图3-124所示；

③利用能量守恒定理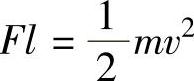求速度，在图3-124中，当触头行程l=0时，速度v_c=0；在触头行程l₁=l_Oe时，速度v可用下式求出：

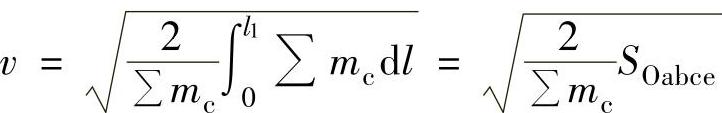
式中 S_Oabce——Oabce所包围的面积。

2）质量的归算：归算的原则是归算前后元件具有的动能相等。

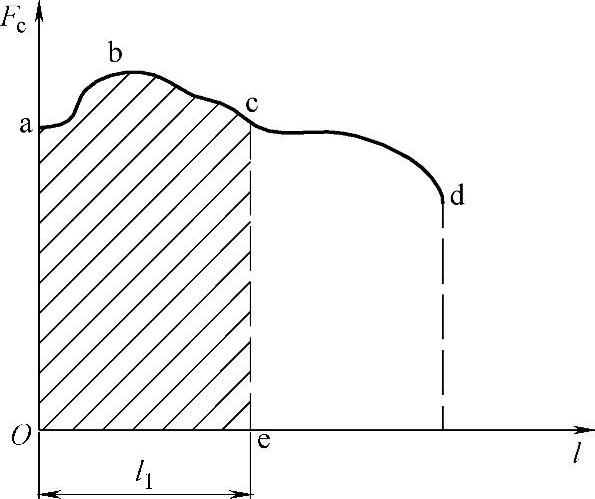
图3-124 归算力∑F_c与触头行程的关系

①做直线运动的元件：设元件的真实质量为m，其运动速度为v，元件具有动能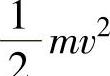，如果归算点的速度为v_c，则归算质量为m_c=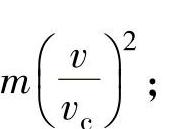

②做旋转运动的元件：设元件的转动惯量为J，若归算角速度为ω，元件具有的动能为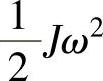，若归算点的速度为v_c，则归算质量为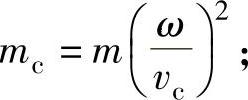

③做平移运动的元件：它既有直线运动又有旋转运动，可分解成直线运动和旋转运动两部分来计算。

3）力的归算：如图3-125所示，力F在C点的归算力F_C可按位移法求得

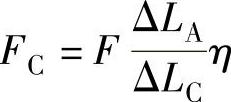
式中 ΔL_A——A点在F作用力方向的位移；

ΔL_C——在A点位移为ΔL_A时，C点相应的位移；

η——效率。

（6）机械传动

断路器及其操作机构的机械传动方式以连杆机构的应用最为普遍。四连杆机构是最常用的一种，很多其他形式的机构都是由它演变而来的。凸轮机构虽不是连杆机构，但在分析力与运动时，在每一位置都可视为一等效的四连杆机构，如图3-126所示。

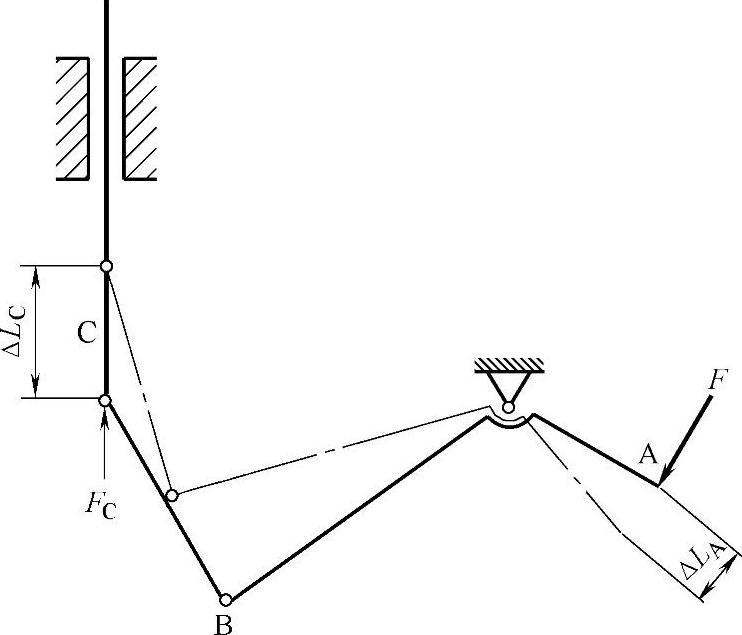
图3-125 力的归算示例

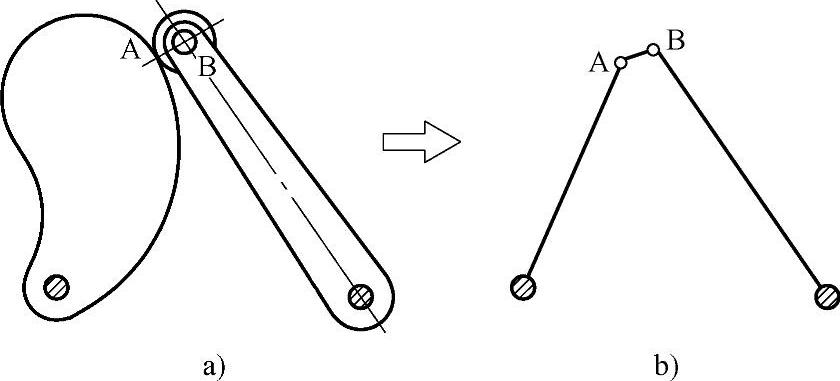
图3-126 凸轮机构与其等效的四连杆机构

a）凸轮机构 b）等效的四连杆机构

1）不考虑摩擦力时四连杆机构的特性：

a.传动比

传动比C是从动轴与主动轴的角速度之比，可用图解法求取，如图3-127所示。传动比

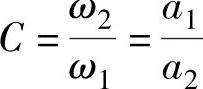
式中 ω₁、ω₂——主动轴与从动轴的角速度（rad/s）；

a₁、a₂——主动轴与从动轴至连杆的垂直距离（m）。

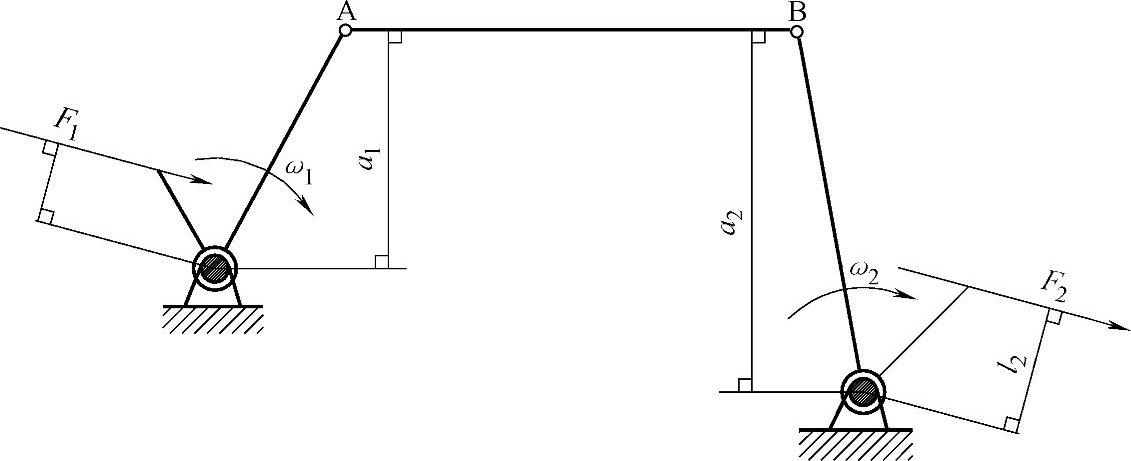
图3-127 图解法求传动比

传动比随机构的位置变化而改变。

b.机械利益

机械利益A_F是连杆AB处于平衡状态时，机构的输出力F₂（见图3-127）与主动力F₁的比值，即

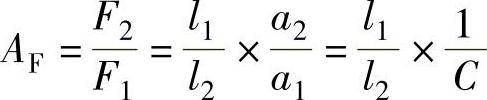
输出力矩M₂与主动力矩M₁的比值，称为力矩机械利益，以A_M表示，

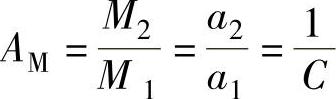
由上述可知，不计损耗时力矩比与传动比成反比例：传动比最大时，力矩比最小；传动比最小时，力矩比最大。

2）考虑摩擦力时四连杆机构的特性：

a.摩擦圆

在平面铰接四连杆机构中，在铰接运动副上存在着摩擦损耗。根据摩擦圆的原理，摩擦力的作用可视为反抗原动力矩的一种反力矩，这个反力矩等于作用在转轴上的正压力F乘以摩擦圆半径ρ，摩擦圆半径ρ又是摩擦系数f与轴销半径R的乘积（见图3-128），受力F作用的连杆要能绕轴转动，必须让力臂a大于摩擦圆半径ρ。开关设备中常用材料的滑动摩擦系数见表3-8。滚动轴承的摩擦系数为0.002～0.02。

b.连杆的力作用线及机械利益

因有摩擦，连杆的力作用线不和连杆轴线重合，而是切于两轴销的摩擦圆，如图3-129所示，其机械利益相对减小。

c.效率

传动机构的效率，是指输出功与输入功的比值。四连杆机构的效率与材料的摩擦系数、连杆的长度、杆件之间的夹角及轴销的直径等有关，当其余因素不变时，效率随杆件之间的夹角的变化而变化，如图3-130所示。值得注意的是，一般情况下，无论四连杆机构处于何种位置，若运动方向相反（例如由合闸变为分闸），它们的效率不同。

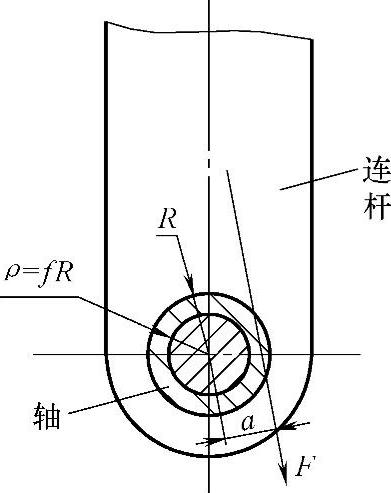
图3-128 摩擦圆示意图

图3-129 考虑摩擦力时力的作用线

要提高传动机构的效率，需设法降低摩擦系数f，如在轴上采用滚动轴承；尽可能地减小轴销的直径；尽量减少相连的四连杆机构的数量。

在断路器本体及其配用的机构中，每一组采用轴销的四连杆的平均效率可粗略地取为0.7～0.9。

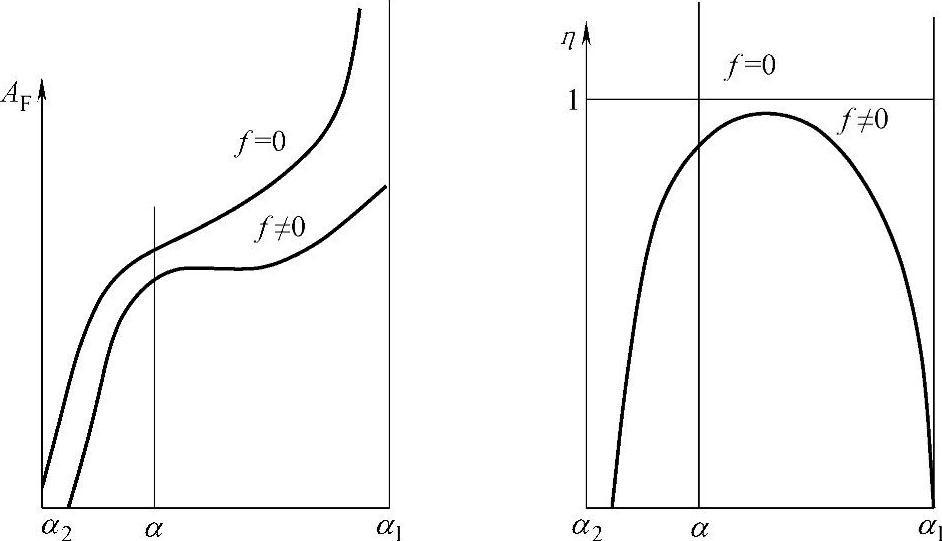
图3-130 四连杆机构机械利益A_F及效率η与转角α的关系

表3-8 常用材料的滑动摩擦系数

图3-131 四连杆的死点（死区）位置

a）不考虑摩擦力时的死点位置 b）考虑摩擦力时的死点位置

3）死点与死区：在某些四连杆机构中，主动杆转动到某一位置时，从动杆的力矩为零。当不考虑摩擦力时，这种位置出现在连杆与从动杆处在同一条直线上时，力的作用线通过从动轴的中心，因此输出力矩为零，如图3-131a所示。此时，如果从动杆没有惯性运动，不论主动杆有多大的输入力矩，从动杆都不会产生转动，这种位置称为死点位置，它的特征条件是力矩机械效益A_M=0。

当考虑杆件中的摩擦力时，由于摩擦力矩的影响，连杆和从动杆在未达到直线位置以前，从动杆的有效力已降低到零，连杆位置上出现了死区，如图3-131b所示。在死区范围内，机构的运动具有不稳定性。

在断路器的设计中，常用死点（区）达到以下目的：

①在合闸过程后期起省力作用。合闸过程触头闭合及缓冲起作用时，阻抗力矩突然增大，利用死区附近传动的特点使主动杆受力小，可用较小的力使断路器合闸。

②利用死区传动的单向性，防止触头在合闸位置上意外跳开（如短路电动力、震荡力的作用等）。其作用原理与上节所述相同。

③分合闸时减少脱扣力、脱扣功。